LFSR和特征函数
测试课程碰到了随机向量生成方面的内容，碰到了线性反馈移位寄存器（Linear Feedback Shift Registers，LFSR）。课件上只简单提了一下，但没有说EE和IE两者结构的区别，以及对应特征函数的作用。全网搜了一通，也没看到说清楚的，最后还是在bing上搜到一篇比较好的课件，特来记录一番。LFSRs
一、LFSR是什么
LFSR有两者类型，外部反馈型和内部反馈型：
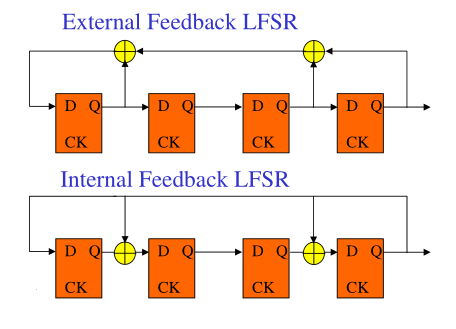
两个电路明显的区别是，EF只更新最后一位，其余移位，且关键路径更长；IF不单纯移位，关键路径更短。
给定初始状态，每个周期会有新的输出，如果选择特定的反馈电路，那么寄存器组成的向量可以遍历除0向量外的其他$2^n-1$个向量，单端的输出便是以$2^n-1$为周期的伪随机数，因此这种电路经常用做伪随机数发生器，IF LFSR也会用来做CRC的编解码。
假设初始状态是1000，那么两个电路寄存器的更新序列如下：
| 序号 | EF | IF |
|---|---|---|
| 1 | 1000 | 1000 |
| 2 | 1100 | 0100 |
| 3 | 1110 | 0010 |
| 4 | 0111 | 0001 |
| 5 | 0011 | 1101 |
| 6 | 0001 | 1110 |
| 7 | 1000 | 1000 |
两个电路的周期都是6，但如果更换电路，那么序列周期大不一样：
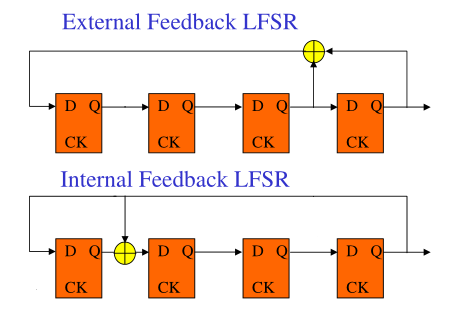
| 序号 | EF | IF |
|---|---|---|
| 1 | 1000 | 1000 |
| 2 | 0100 | 0100 |
| 3 | 0010 | 0010 |
| 4 | 1001 | 0001 |
| 5 | 1100 | 1100 |
| 6 | 0110 | 0110 |
| 7 | 1011 | 0011 |
| 8 | 0101 | 1101 |
| 9 | 1010 | 1010 |
| 10 | 1101 | 0101 |
| 11 | 1110 | 1110 |
| 12 | 1111 | 0111 |
| 13 | 0111 | 1111 |
| 14 | 0011 | 1011 |
| 15 | 0001 | 1001 |
| 16 | 1000 | 1000 |
这两个电路反馈的位置有某种对称性，是否有方法直接判断电路的周期数呢，或者该如何设计电路，让其产生$2^n-1$周期的伪随机数？
二、特征函数
多亏了数学家们的努力，这种LFSR电路可以用特征多项式的形式表示：
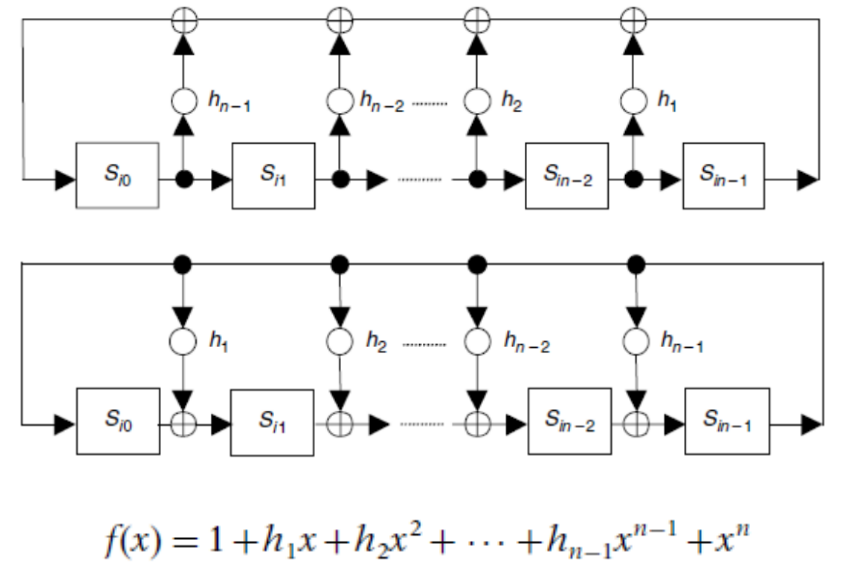
上面两个例子(图1、图2)对应特征多项式分别是：
$$ \begin{aligned} f_1(x)&=x^4+x^3+x+1\\ f_2(x)&=x^4+x+1 \end{aligned} $$ 那么特征多项式有什么用呢？ ### 1、判断周期 第一种电路的周期是6，我们可以验证：$x^6+1$能被$f_1(x)$整除： $$ x^6+1=(x^4+x^3+x+1)(x^2+x+1) $$ 注意这里的“加法”是异或逻辑，相同指数项相加，偶数个为0，奇数个为1，如$x^3+x^3=0,x^2+x^2+x^2=x^2$。 同理，第二种电路的周期是15，可以验证：$x^{15}+1$能被$f_2(x)$整除： $$ x^{15}+1=(x^4+x+1)(x^{11}+x^8+x^7+x^5+x^3+x^2+x+1) $$2、计算下一个向量序列
对于IE结构，如果当前向量为$S_0$，那么下一个向量$S_1$既可以通过电路得到，也可以由多项式得到：
$$ S_1=(S_0 *x) \% f(x) $$ 比如$S_0=0011=x^2+x^3$，那么： $$ S_1=(x^2+x^3)x \% (x^4+x+1)=(x^4+x^3)\%(x^4+x+1)=x^3+x+1=1101 $$ ### 3、由本征f(x)构造伪随机数电路
如果我们想产生周期为$2^10-1=1023$的伪随机数，那么可以取本征多项式$f(x)=x^{10}+x^3+1$，得到相应EF或IF电路。
三、EF和IF关系
有一个奇怪的问题是，上面定义的EF和IF的电路从时序上看，它们产生序列的顺序并不一样，那么它们为什么对应相同的特征多项式？
这张图给出了答案：
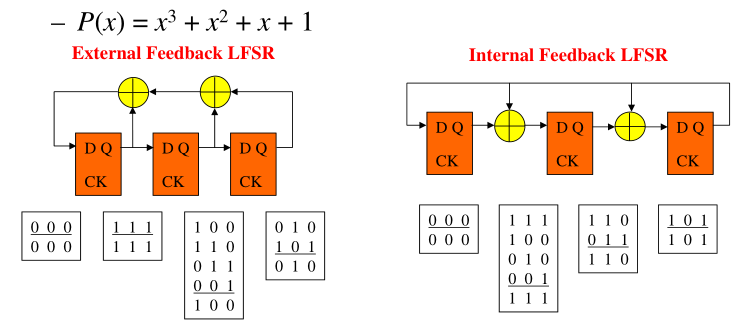相同的特征多项式表示电路产生的各类周期是一样的，它表示更抽象层面的相同结构，比如上述电路可以分为两个1周期，一个2周期，一个4周期的情况，总共是8种状态。