密码学笔记(一)
近期学习密码学，希望用一些具体例子帮助如何自己快速回顾其精髓。
引言
通信过程中，为了保证信息安全，通常需要加密，加密是明文和密钥在加密算法（Cipher）的作用下，生成密文。从加密算法的演变来看，依次出现经典密码学，现代密码学，非对称密码学。从密钥分发的角度看，可以分出传统密钥分发和量子密钥分发，即量子密码学。
对称密钥加密时，如果黑客截取密文，并知道加密算法（如AES，Advanced Encryption Standard），如果不知道密钥，也很难通过计算机数学暴力破解。其面临的问题是，如何保证对方安全得收到密钥？这是密钥分发难题。
为此，出现了非对称加密，利用公钥和私钥巧妙地解决了密钥分发问题，由此开辟了密钥学研究的新方向。虽然解决了密钥分发问题，但其算法相对于AES还是更可能被数学破解。是否有一种方法，既可以解决密钥分发，又可以达到很强的数学保密性？微观粒子的量子效应恰恰具备这种潜力，这将在第三部分具体介绍。
各部分简介
第一部分主要介绍对称密码算法在历史的博弈中是如何变得越来越复杂，计算机的加入将经典密码学带入现代阶段。
第二部分针对密钥分发问题，提出非对称加密的解决方案，著名的非对称加密算法有：Elgamal（基于离散对数）、RSA（基于大数分解）和ECC（椭圆曲线加密算法）。
第三部分巧妙应用光子的量子效应，解决对称密钥的分发问题，理论上达到安全通信的新阶段，几乎无法数学攻击破译。
一、对称密钥加密
经典密码学
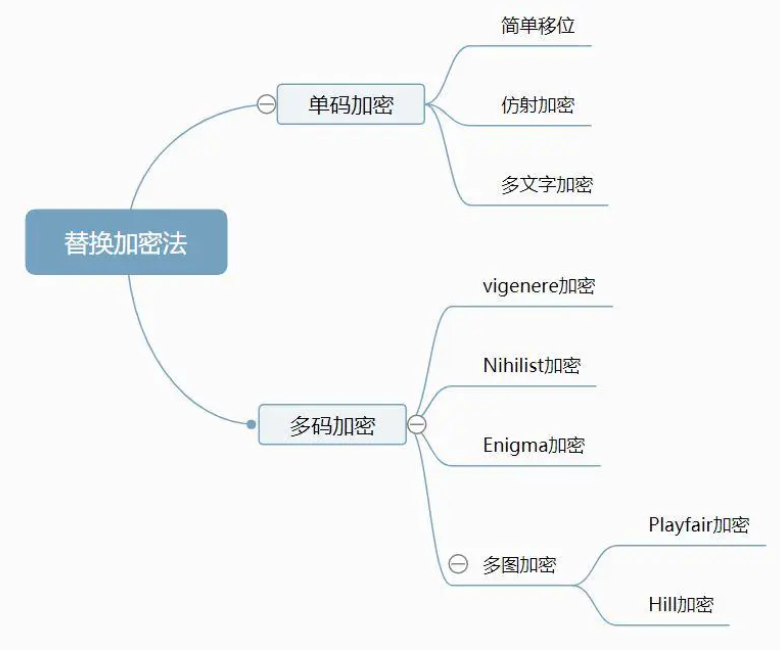
1、替换加密（substituttion）
以凯撒加密为例： 加密算法：每个字母向前移动3位（密钥） 比如：hello->ehoor。 说明：凯撒加密属于替换加密这一大类的一种，每个原文字母唯一映射另一个字母作为“替换”。但这种算法可以通过频率统计的方法破解，比如e是英文字母中出现频率最高的数字，那么如果把e替换为x，那么x即为密文中出现频率最高的字母，因此可以推断x对应e，可以利用英文字母其他出现规律来破译其他字母。
替换加密图谱：
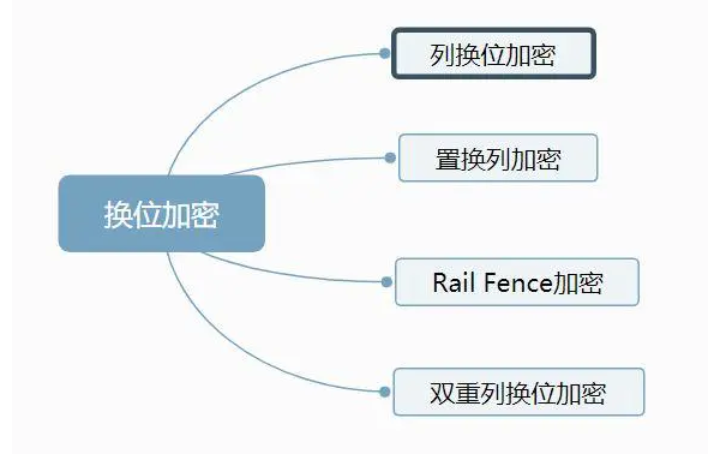
2、换位加密（permutation）
不同于替换，换位加密是改变明文的顺序，所以不能用频率统计法破解。简单的例子是列移位加密。
比如短语“encryption algorithms”可以写入该矩形：
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| e | n | c | r |
| y | p | t | i |
| o | n | a | l |
| g | o | r | i |
| t | h | m | s |
再按一定顺序读取列生成密文，比如4、1、2、3，那么密文就是：“rilis eyogt npnoh ctarm”，如果字母不够，可以添加“x”或“q”无效字母。
破解：a、可以通过字符长度推测矩形的大小，比如一个消息有153个字符，153可分解为3×51、51×3，17×9、9×17。 b、确定正确的矩形，根据明文英文的每行应包含约40%的元音字母，可以推测正确的矩形大小。 c、还原列顺序，“引导字母”法很有帮助。
（详情见《经典密码学和现代密码学》P78）
换位加密图谱：
现代密码学
经典密码学的加密和解密大多数由手工完成，现代密码学是进入计算机加密时代，充分利用计算机善于处理加密复杂性的特性产生的，但其基础仍在经典密码学。
现代密码学主要有流加密法和块加密法，这里主要介绍块加密法中的DES和AES。
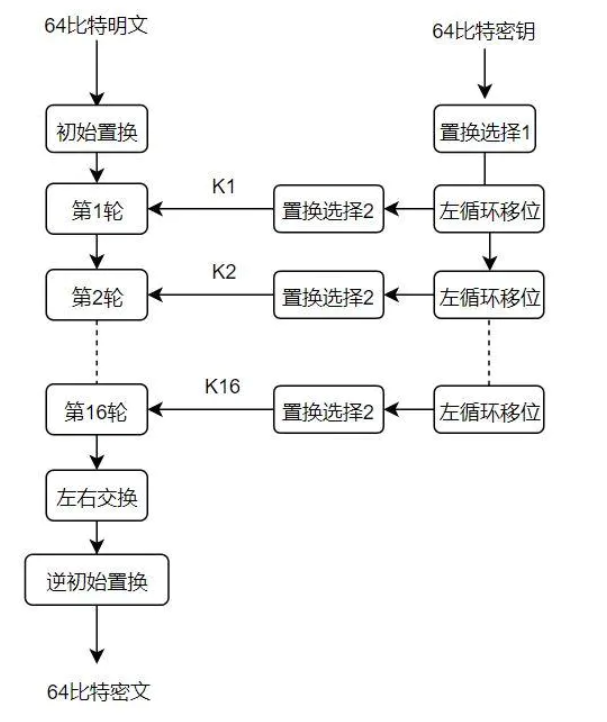
1、DES（Data Encryption Standard）
总框架：
第一步，先看如何从初始64比特密钥得到K1？
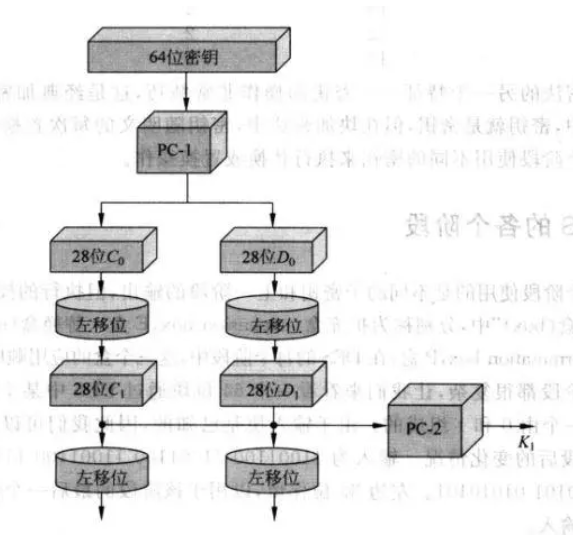
其中PC-1(permuted choice1) 即为置换选择1，它的作用是从初始64位二进制数中选择56位并重新排列：
可以看出，里面没有8、16、24、32、40、48、56、64这8位校验位，原来57位的数值移到了第1位。
$C_0$为前28位，左移1位得到$C_1$，$D_0$为后28位，左移1位得到$D_1$。左移的位数于第几轮有关：
| 轮数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 左移位数 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
PC-2(permuted choice2) 即为置换选择2，它的作用是从$C_1,D_1$合并后的56位二进制数中选择48位并重新排列：
即第14位移到第1位，第17位移到第2位，如是置换。
第二步，再看明文在第一轮经过怎么样的操作？
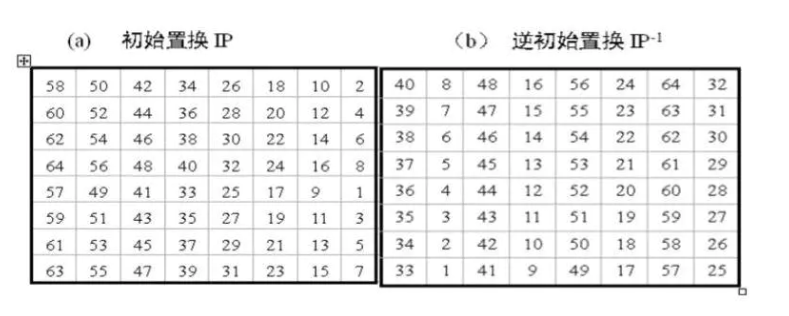
明文先按左到右，上到下的顺序写成表格的形式，经过初始置换进入第1轮，原来58位置的二进制数移到第1位。再看逆置换，原来的40位（左图的40位是1）变为第1位。
置换后的明文分成左32位和右32位，右32位作为输出的左32位，左32位和右32位经过E盒、异或、S盒、P盒的结果异或得到输出的右32位，完成第一轮，如此再重复至16轮：
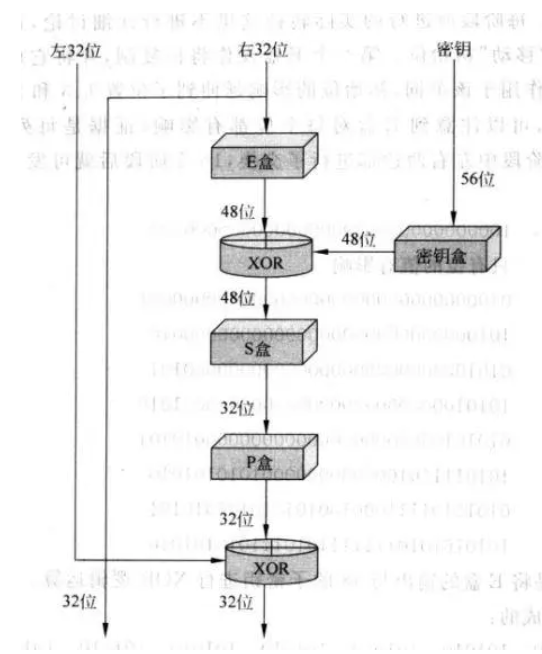
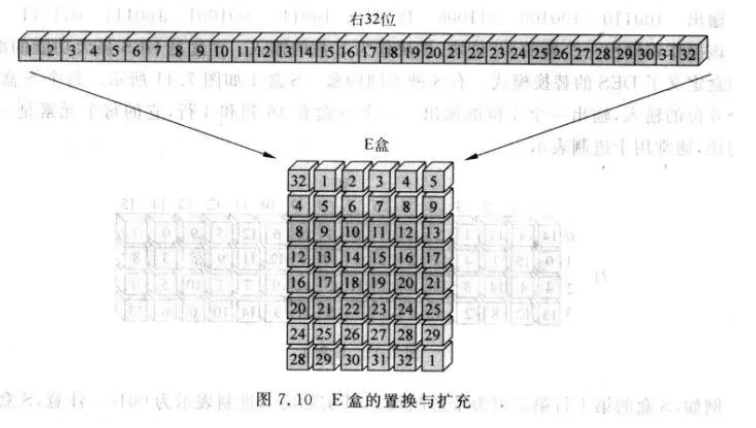
E盒为扩充盒（expansion box）将右32位扩充位48位，在第一轮时与K1异或，再进入S盒。
S盒为替换盒（substitution box）48位分成8组，每组6bit数分别进入8个不同S盒，$x_5x_0$代表行号，$x_4x_3x_2x_1$代表列号，可以对应一个4bit数据。如图101100，表示2行6列，对应2，4位二进制数为0010，实现101100→0010的映射，这种映射是非线性的，也是S盒的魅力所在。
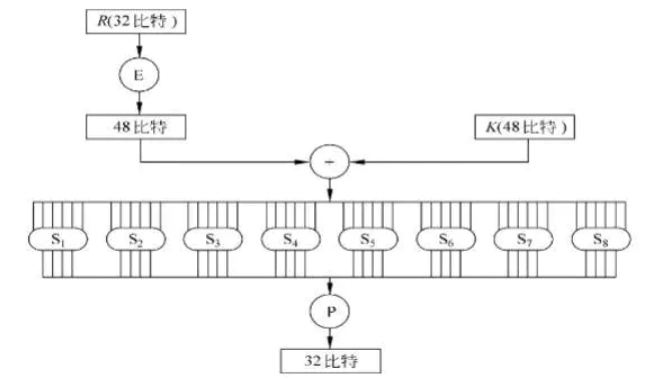
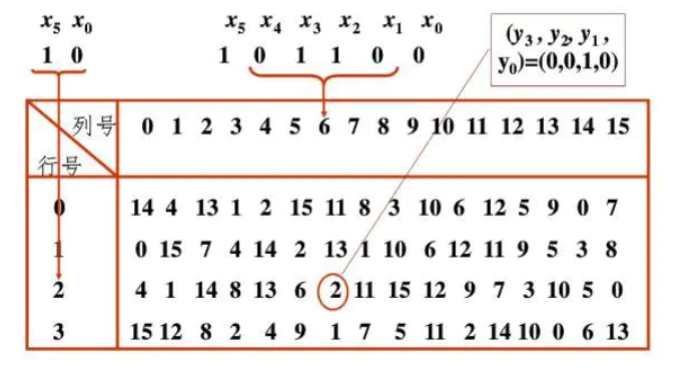
下图是8个具体的S盒：
P盒为置换盒（permutation box）对S盒输出的32位再一次变换顺序，最后与左32位异或即为第一轮新输出的右32位。
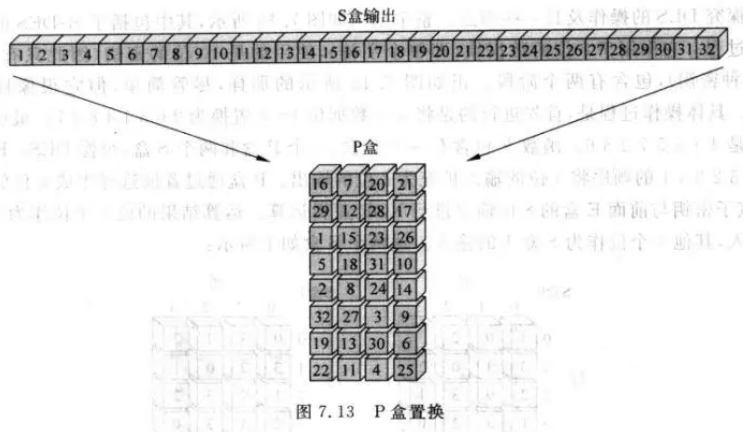
DES（数据加密标准）于1977年由IBM和NSA开发，有效密钥长度为56位（其他8位为校验位），约由72千万亿种不同组合。但到了20年后，随着计算机算力提升，DES可以在两天内暴力破解，因此在2001年提出了AES（高级加密标准）。
####2、AES（Advanced Encryption Standard）
总框架
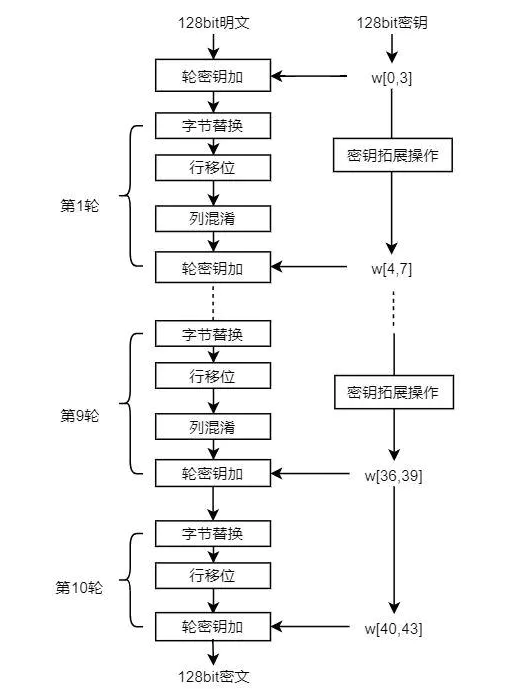以128bit长度的分组为例，经过10轮操作，可以从明文转化为密文，注意第10轮没有列混淆，目的是与解密时形成对称。AES与DES的一个显著不同是，AES替换和置换的单元是字节（8bit），而不是DES中的1bit，这大大提高了破解难度。
第一步的轮密钥加是异或运算，最初的明文与最初的密文异或。128bit是16字节，这16字节可以组成4×4的矩阵，便于后续操作：
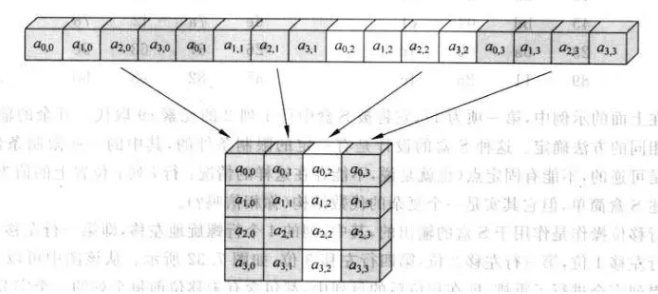$a_{0,0}$是前8位二进制数，可以表示一个ASCII码，也可以用两个16进制数表示，如10001111→8f。
字节替换即进入S盒，可以通过复杂的代数运算得到，也可以通过查表：
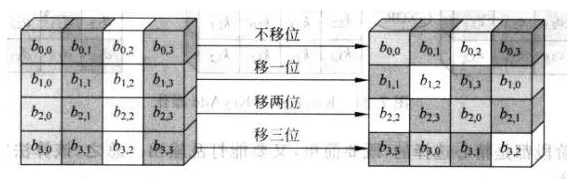
行移位也是以字节位单位的移位，第一行不移，第二行左移一字节，第三行左移两字节，第四行左移三字节：
列混合由矩阵乘法得到$M_{4×4}×B_{4×4}=C_{4×4}$
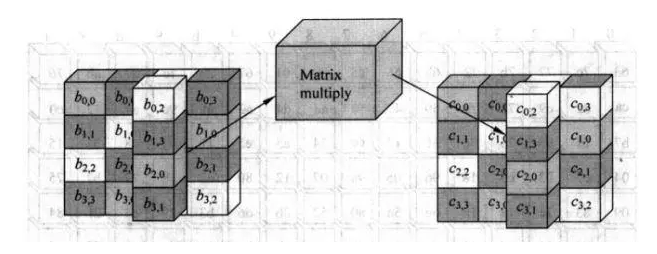比如其中一列是$(11,09,01,35)^T$,经过矩阵M后得到$(73,6b,ba,a7)^T$:
第二个难点是密钥扩展操作，$W[0,3]$为最初的128bit密钥，如何得到$W[4,7]$？设初始密钥$W(0)=3ca10b21,W(1)=57f01916,W(2)=902e1380,W(3)=acc107bd$ $W(4)=W(0) \bigoplus T[W(3)]$ $T[W(3)]$的计算步骤如下： (1)循环地将$W(3)$地元素移位：acc107bd变成c107bdac。 (2)将c107bdac作为S盒的输入，输出为78 85 7a 91。 (3)计算第一轮的常数$r(4)=2^0=01$（以十六进制表示）。 (4)将$r(4)$与第一个字节78进行异或运算：78 \bigoplus 01 = 79。 因此$T[W(3)]=79 85 7a 91$，并且 $W(4)=3ca10b21 \bigoplus 79857a91=452471b0$
其余三个子密钥相对简单： $W(5)=W(1) \bigoplus W(4)=57f01915 \bigoplus 452472b0=12d468a5$ $W(6)=W(2) \bigoplus W(5)=902e1380 \bigoplus 12d468a5=82fa7b25$ $W(7)=W(3) \bigoplus W(6)=acc107bd \bigoplus 82fa7b25=2e3b7c98$ 于是，第一轮密钥操作后为 $452471b012d468a582fa7b252e3b7c98$。
对于128位的密钥，哪怕用现在地球上的所有计算机也要上万亿年的时间才能遍历所有组合。AES的分组长度还可以是192位或256位，带来很大灵活性。
AES为什么不采取更多位数和更多轮数？因为如果这样，加密会更加耗时，没人愿意等几分钟才发送邮件或浏览网页，这是在性能和安全上的一种平衡，如今的AES加密被广泛使用，如iPhone上的加密文件、WPA2协议在WiFi中访问HTTPS网站。