密码学笔记(二)
二、非对称加密
对称密钥既可以用来加密,也可以用来解密,看上去很实用也很方便,但是每个有权访问明文的人都必须具有该密钥,如果一个粗心的用户泄露了密钥,那么就等于泄露了密文,因此密钥的发布成了新问题。针对这一问题的解决方案是,公钥加密算法,属于非对称加密。
这种加密算法有两个不同的密钥:一个用来加密,另一个用来解密。加密密钥可以是公开的,只有解密密钥是保密的。
1、RSA
假设Alice要给Bob发消息,Alice先利用Bob的公钥(全网公开)对消息加密,发送给Bob后,Bob用其私钥对消息解密。如果Bob需要反馈Alice,则Bob要利用Alice的公钥(不同于Bob的公钥)对消息加密,然后发送给Alice,最后Alice用她自己的私钥解密读取消息。
比如Alice给Bob发送消息“Hi”,该消息在ASCII中用16位进制表示为01001000 01011001,转化成十进制为72,105。然后Alice用Bob的公钥(139,253)加密:
$$ 72^{139} \mod {253}=2, 105^{139} \mod {253}=101 $$ Bob接受到消息(2,101)通过私钥(19,253)解密: $$2^{19} \mod {253}=72,101^{19} \mod {253}=105 $$ 将两个数转换成二进制并查ASCII表得到消息“Hi”。那么私钥和公钥是如何得到的呢?先选择两个素数,如$p=11,q=23$,确定$n=pq=253$,接下来确定私钥$d$,满足$d$与$(p-1)(q-1)=220$互质,这样的数很多,不妨取$d=19$。最后确定公钥的另一部分$e$,满足:
$$ 19e \mod{220}=1 $$ 解得$e=139$。这样公钥为(139,253),且全网公布,私钥(19,253)中的19只有Bob知道。 #### 2、ElGamal算法 同样,比如Alice向Bob发送消息“Hi”,在ASCII表中对应十进制为72,105。然后Alice用Bob的公钥(p=13171,g=2,y=11852)加密,不同于RSA,这里一个明文会产生两个数组成的密文:(下面的$r_1,r_2$为随机数) $$ c_1=g^{r_1} \mod p = 2^{31} \mod {13171}=4782 $$ $$ c'_1=m_1 y^{r_1} \mod p = 72×11852^{31} \mod {13171}=7565 $$ $$ c_2=g^{r_2} \mod p = 2^{16} \mod {13171}=12852 $$ $$ c'_2=m_2 y^{r_2} \mod p = 105×11852^{16} \mod {13171}=2072 $$ 因此Alice将密文(4782,7565)、(12852,3898)发给Bob,Bob利用私钥$x=23$解密: $$ (c'_1/c^x_1)\mod p=(7565/4782^{23})\mod {13171}=72 $$ $$ (c'_2/c^x_2)\mod p=(3898/12852^{23})\mod {13171}=105 $$ 那么公钥和私钥是如何生成的呢? 1、找一个较大的素数$p$,例子中是13171; 2、找$g$,它是$Z_p^*$中的生成元,例子中是2; 3、选一个私钥$x$,小于$p-1$的整数,例子中是23; 4、确定公钥$y=g^x \mod p$,例子中是11852。 这样(p,g,y)为公钥,x为私钥。加密时还需要生成一个随机数,它对解密没有影响。ElGamal加密法引入了一些新的特征,最显著的是引入随机数,这意味这相同的明文可以有不同的密文,提高了安全性。但是由于密文是明文的两倍大,从而增加了对存储空间的需求,降低数据传输的速度。
3、ECC(Elliptic Curve Cryptography )
椭圆曲线密码体系不像前两个算法一样直接,需要先具备一些数学基础,有一篇不错的科普文:椭圆曲线密码体制。
先看一个具体例子吧,假设Alice要把消息“3”发给Bob: 1、Bob先选定一条椭圆曲线,并取椭圆曲线上一点作为基点G。比如$E_{29}(4,20)$,基点$G(13,23)$,基点G的阶数n=37。
$$ E_{29}(4,20):y^2=x^3+4x+20 \mod 29 $$ G点在椭圆曲线上: $$ 13^3+4×13+20 \equiv 23^2 \equiv 7 \mod 29 $$ 阶数为n=37表示: $$ 37 G =O_{\infty} $$ 椭圆曲线上的加法和乘法规则可以参考: [ECC椭圆曲线详解](https://www.cnblogs.com/Kalafinaian/p/7392505.html "ECC椭圆曲线详解(有具体实例)") 2、Bob选择一个私钥k(k三、量子密码学
我们前面介绍了AES算法,如果Alice现在要发送消息给Bob,她发现之前的密钥可能被盗取,希望换一个新密钥,那么如何将这个密钥告知Bob并不让黑客发现呢?这其实像一个悖论,如果可以安全的传输密钥,那么岂不是也能安全的传输明文,也就不用加密了。
山重水复疑无路,柳暗花明又一村
量子密码学恰恰提供了解决方案,而且它只能安全地传输随机数,但不能传输特定的明文,而随机数刚好可以用来作为密钥加密,完美对接!
那么该用什么样的媒介传输密钥,并且具有量子效应呢?光子!BB84协议就是使用光子,它能容易地在光纤链路中实现。它将二进制位0和1按光子地偏振(电场的方向)加密。光子可以在水平、垂直或对角线(+45°和-45°)发生偏振,如下图:
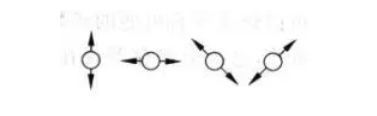
接下来的特性很关键,当光子输入不同的滤波器时,其输出会因为滤波器的不同而呈现不同的特点。滤波器有两种:水平垂直滤波器和斜线滤波器。当水平偏振光子通过水平垂直滤波器时,其状态不变;但通过斜线滤波器时,它将随机地变为+45°或-45°的偏振光,如图
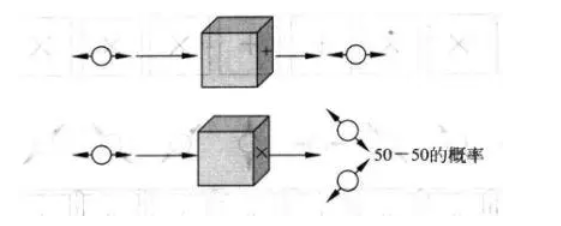
在发送密钥之前,我们先定义“0”表示垂直或+45°方向偏振的光子,1表示水平或-45°方向偏振的光子,这一点很重要:
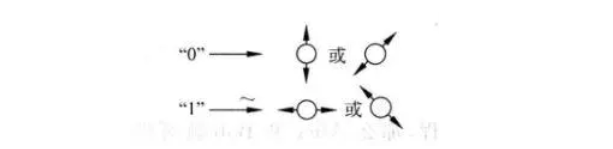
最后是见证奇迹的时候,假设Alice生成10个随机数:1101000100(这还不是最终的密钥),无序的光子可以通过-45°过滤器得到-45°的偏振光,即发送“1”,通过垂直的过滤器得到垂直偏振光,也发送“1”。Bob在接收端可以随机选择偏振过滤器(x为斜线,+为水平垂直方向),如:+xx__xxx+x,因此他得到的序列是1001010101。他再与Alice通电话(无惧偷听),确定Bob哪个滤波器是对的,比如这里是3、4、5、7、8、9位正确,这样他们就确定了密钥010010。详细过程如下:
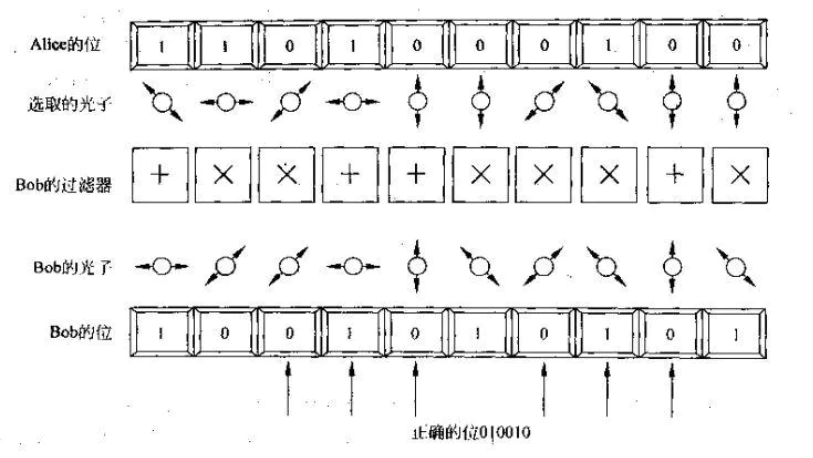
这种方式可以防止黑客的窃听,如果他也用滤波器截取Alice的发送序列,那么会破坏其状态,能被Bob和Alice发现,而且黑客也不能复制Alice的光子,因为量子系统具有不可复制性。
量子密钥发布(Quantum key distribution。QKD)已经在实验室得到了实现,Los Alamos国家实验室在48km光纤上演示了QKD的过程。日内瓦大学构建的QKD实验中,光纤长达70km,速率为100Hz。2016年8月16日,墨子号量子卫星上天,光纤中的安全传输超过了200km,间隔100km的量子保密电话已经在技术上可行了,但还需要进一步工程设计才能商用。
##参考资料: 《经典密码学和现代密码学》 计算机科学速成课-加密 你完全理解的量子信息 中国MOOC-电子科技大学-现代密码学