忆阻器（二）——忆阻模拟器
除了真实的器件，我们也可以用运放和乘法器来搭忆阻模拟器。这节将介绍数学模型、matlab仿真及multisim仿真。
一、数学模型
忆阻分为磁控和荷控两种，这里介绍三次非线性磁控忆阻模型：
$$ \begin{cases} I=W(\varphi)V \\ W(\varphi)=a+3b \varphi ^2\\ \frac{d \varphi }{dt}=V \end{cases} $$ 这里的$W$为忆导。假设电压为正弦波动$V(t)=V_m\sin(\omega t)$，积分可得磁通量：
$$ \begin{aligned} \varphi(t)&=\int_{-\infty}^t V(\tau)d\tau=\varphi_0+\int_0^t V_m\sin(\omega \tau)d\tau\\ &=\varphi_0+\frac{V_m}{\omega}[1-\cos(\omega t)] \end{aligned} $$ 带入电流表达式可以得到： $$ \begin{aligned} I(t)&=\{a+\frac{3b}{\omega^2}[\varphi_0\omega+V_m-V_m\cos(\omega t)]^2\}V_m\sin(\omega t)\\ &=c_1\sin(\omega t)+c_2\sin(2\omega t)+c_3\sin(3\omega t) \end{aligned} $$ 其中$c_1=(a+3b\varphi_0^2+\frac{6b}{\omega}V_m+\frac{15b}{4\omega^2}V_m^2)V_m$，$c_2=-\frac{3b}{\omega^2}(\varphi_0 \omega+V_m)V_m^2$，$c_3=\frac{3b}{4\omega^2}V_m^3$。二、matlab仿真
假设系统参数$a=0.6667mS,b=194.4945 S/Wb^2$，可以得到不同条件下电流$I(t)$随电压$V(t)$的变化关系：(代码见附录)
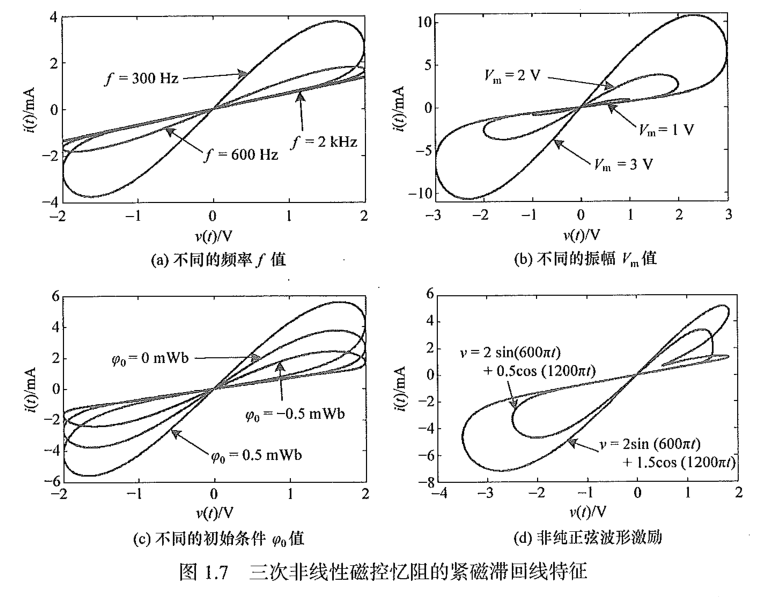
三、基于运放和乘法器的忆阻模拟器
1、原理推导
忆阻模拟器的原理图如下：
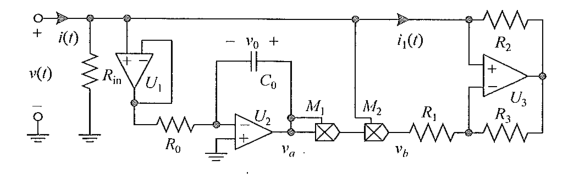
包含3个运放、2个乘法器、1个电容和5个电阻。第一级放大器$U_1$用于避免负载效应；第二级放大器$U_2$与电阻$R_0$和电容$C_0$构成积分器：
$$ v_a(t)=v_0(t)=-\frac{1}{R_0C_0}\int_{-infty}^t v(\tau)d \tau =- \frac{1}{R_0C_0}\varphi(t) $$乘法器$M_2$的输出电压：
$$ v_b(t)=g_1g_2[v_a(t)]^2v(t) $$ $g_1,g_2$分别表示$M_1,M_2$的增益。第三级放大器$U_3$与$R_1,R_2,R_3$构成电流反转电路，当$R_2=R_3$时，可以得到：
$$ i_1(t)=-\frac{v(t)-v_b(t)}{R_1}=\{-\frac{1}{R_1}+\frac{g_1g_2[v_a(t)]^2}{R_1}\}v(t) $$最后得到输入端电流：
$$ i(t)=\{(\frac{1}{R_{in}}-\frac{1}{R_1})+\frac{g_1g_2[v_a(t)]^2}{R_1}\}v(t) $$等效忆导的表达式为：
$$ W(\varphi)=\frac{1}{R_{in}}-\frac{1}{R_1}+\frac{g_1g_2}{R_1(R_0 C_0)^2}\varphi^2 $$ 与数学模型对比可以得： $$ \begin{cases} a= \frac{1}{R_{in}}-\frac{1}{R_1}\\ b=\frac{g_1g_2}{3R_1(R_0 C_0)^2} \end{cases} $$2、仿真
设定放大器的工作电压为$\pm 15V$，磁控忆阻的等效参数$a=0.6667mS,b=194.4945 S/Wb^2$，进而得到电路参数：
| 电路参数 | 物理含义 | 参数值 |
|---|---|---|
| $C_0$ | 电容 | 47nF |
| $R_0$ | 电阻 | $8.2k\Omega$ |
| $R_1$ | 电阻 | $750\Omega$ |
| $R_2$ | 电阻 | $1.5k\Omega$ |
| $R_3,R_4$ | 电阻 | $2k\Omega,2k\Omega$ |
| $g_1$ | 尺度因子($M_1$) | 0.1 |
| $g_2$ | 尺度因子($M_2$) | 1.3 |
multisim搭好电路图：
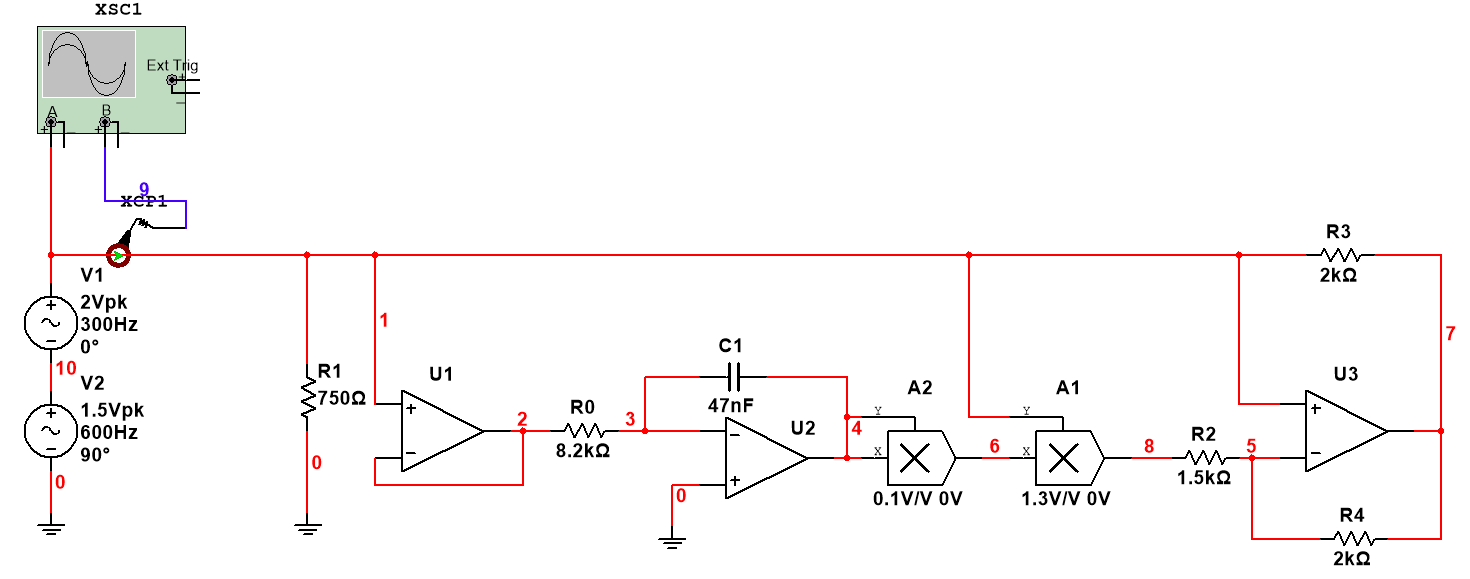改变参数，可以得到不同的电流——电压变化图：
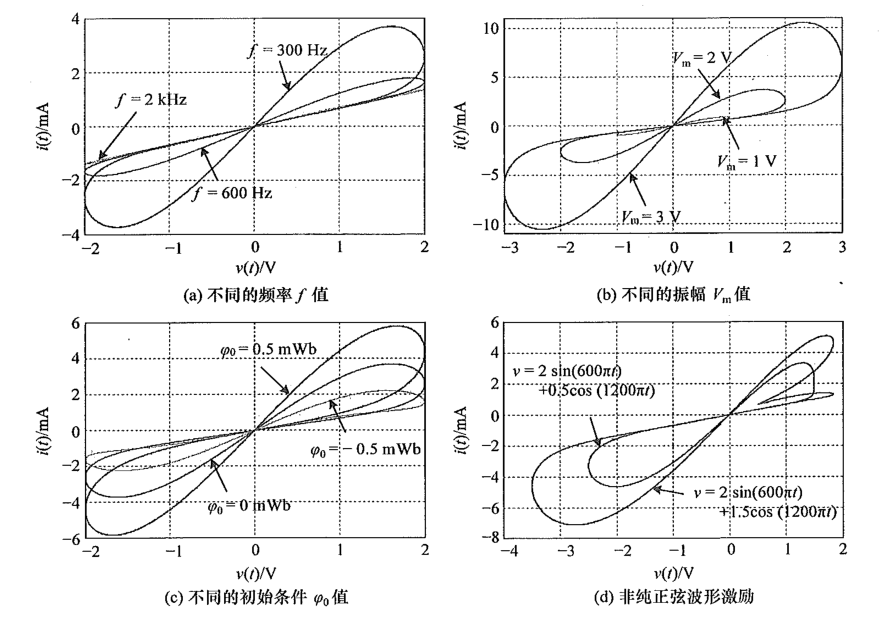
这里选取最后一个例子：
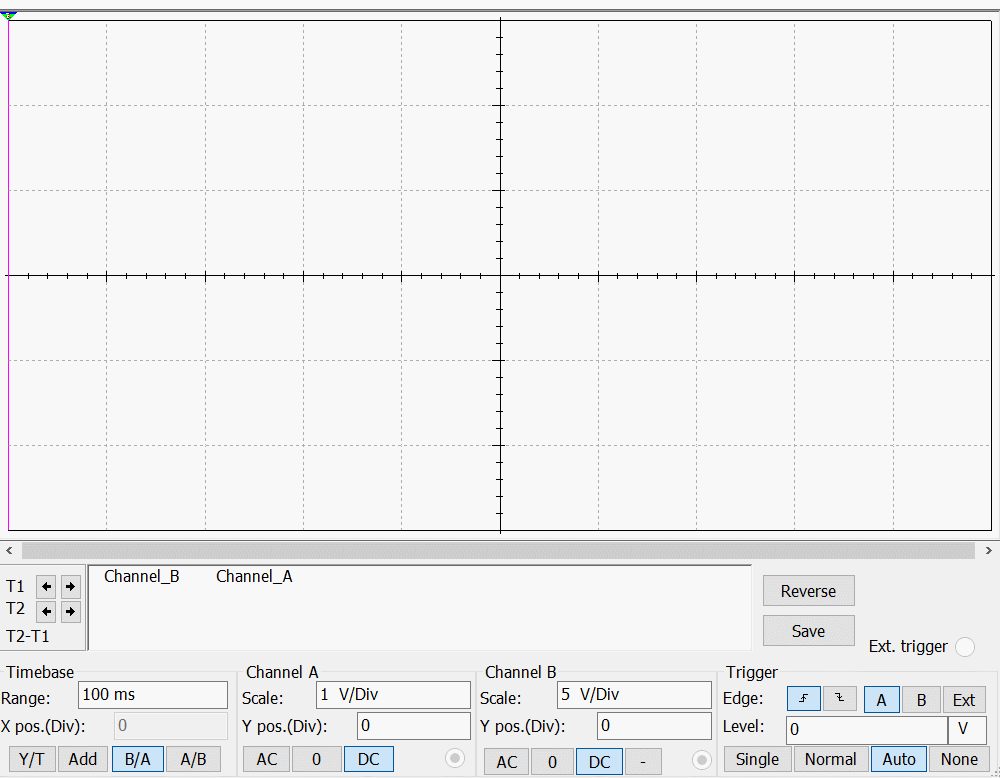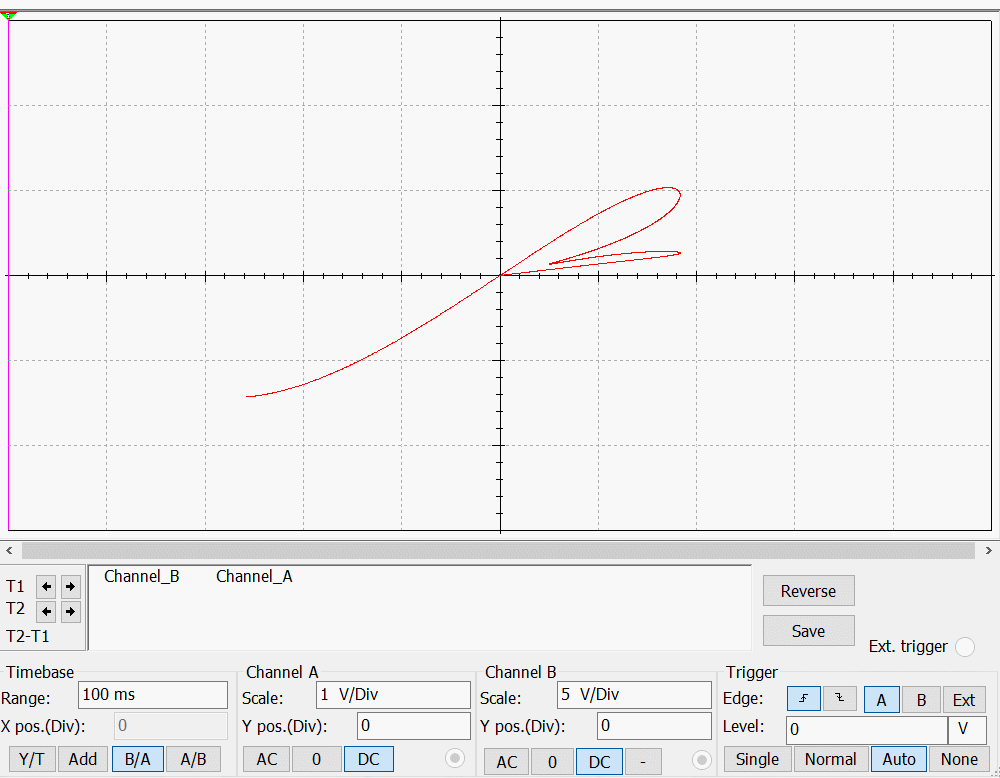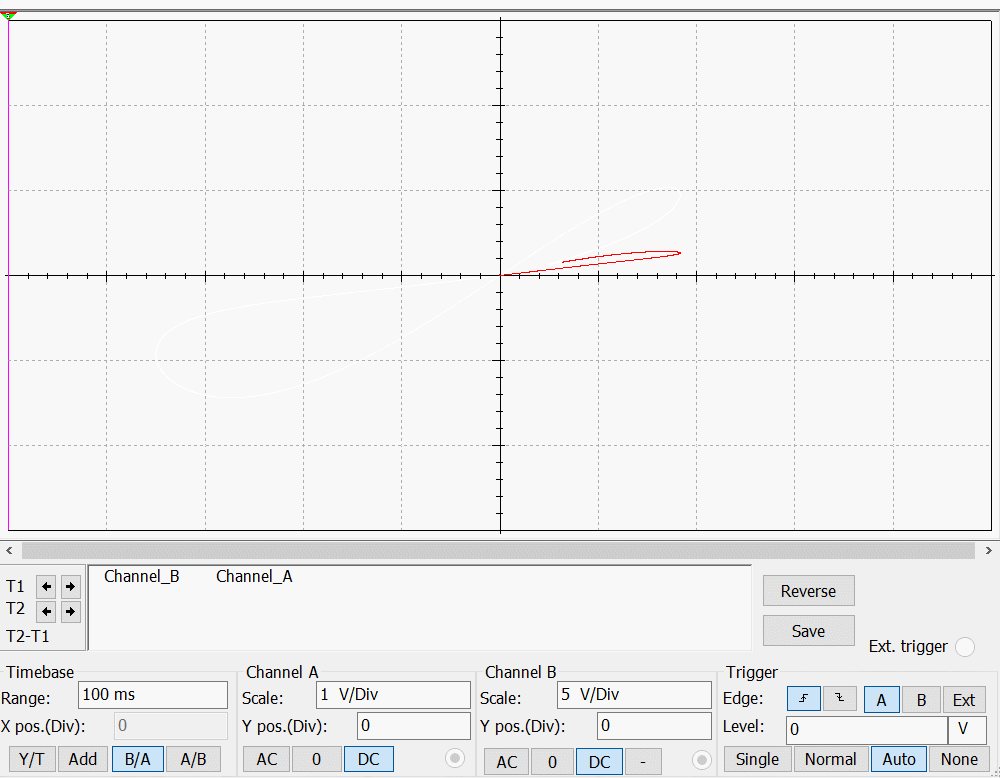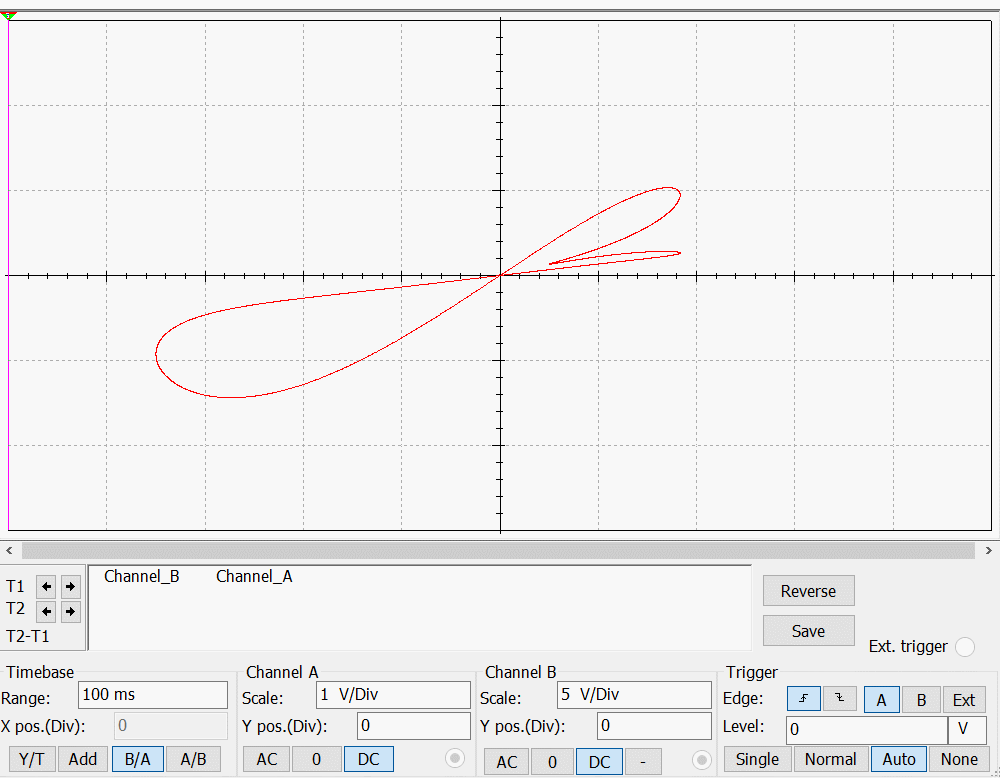
附录
% 1.basic parameter
clear;clc;
a = 0.6667 * 10^(-3);
b = 194.4945 ;
% vm = 1,2,3
vm = 1;
% fai0 = 0,-0.5,0.5 m Wb
fai0 = -0* 10^(-3);
% f = 300,600,2000Hz
w = 2*pi*300;
% 2.time
t = linspace(0,2*pi/w,1001);
delta = 2*pi/w/1000;
% 3.it,x,M,V
vt = vm*sin(w*t);
%vt = 2*vm*sin(w*t)+1.5*vm*cos(2*w*t);
N = size(t);N = N(2);
fai =vt;
for k=2:N
fai(k)=vt(k)+fai(k-1);
end
fai = fai0 + delta *fai;
W = a+ 3*b*fai.^2;
I = W .*vt;
plot(vt,I);
您好，我尝试复现了这个忆阻电路图，图是一模一样的，但是示波器显示的不一样，可以给我一份源文件吗。
会不会是你选的电容默认有寄生电阻
源文件早不在了，这东西之后都没碰了
大佬现在搞什么方向