Matlab如何用均匀分布产生其他分布？

背景

Matlab有一个随机数生成函数rand(1,n)，即在(0,1)区间产生均匀分布的n个随机数。如果需要在带权重的蒙特卡洛模拟中生成其他概率密度分布的随机数，该怎么办呢？能够利用均匀分布经过某种变换得到吗？

这篇笔记就是介绍如何利用均匀分布，产生其他分布，比如概率密度：

$$ f(y)=(4-2y)/3 ,y\in[0,1] $$ 具体目的是先用matlab生成[0,1]的100个随机数，然后通过什么变换，将这100个随机数做映射，而其统计结果符合上述的概率密度分布。这样做有什么意义吗？一方面能加深对概率密度间转换的理解，你会发现考研数学中统计与概率终于有用武之地！另一方面，我们如果能够产生自己所希望的概率分布的随机数，在[带权重的蒙特卡洛模拟](https://www.jianshu.com/p/6b34474fded8)中会如虎添翼，大大提高效率。

一、标准流程介绍

设随机变量X的概率分布为U(0,1)，若$Y=h(X)=X^2$，求Y的概率密度分布？

先计算Y的累计分布函数，再对其求导得到Y的概率密度函数：

$$ F(y)=P(Y\leq y)=P(X^2\leq y)=P(X\leq \sqrt{y})=\sqrt{y},y\in(0,1) $$ $$ f(y)=\frac{d F(y)}{d y}=\frac{1}{2\sqrt{y}},y\in(0,1) $$ 这套流程非常标准化，也很实用，那么现在的问题是：已知f(y)，如何求出h(X)?

二、实战

设随机变量X的概率分布为U(0,1)，若$Y=h(X)，f(y)=(4-2y)/3 ,y\in(0,1)$，那么h(x)为多少？

如果不清楚前面的标准流程，这种题目绝对会一头雾水，也多亏了考研时这方面的训练，能够比较清晰的获得解答：

$$ F(y)=P(Y\leq y)=P(h(X)\leq y)=P(X\leq h^{-1}(y))=h^{-1}(y) $$ 另一方面： $$ F(y)=\int_0^y f(y) dy=\frac{1}{3}(4y-y^2),y\in(0,1) $$ 因此需要解一个反函数： $$ h^{-1}(y)=\frac{1}{3}(4y-y^2) $$ 令$h^{-1}(y)=x$，再反解y即可，这里有点绕，需要细细品味： $$ y=2-\sqrt{4-3x}=h(x) $$ 即为所求的映射关系。 ## 三、直观呈现

% matlab 代码
clear;clc;
%产生n个(0,1)的随机数
n=10000;
x=rand(1,n);
%x的概率密度统计图
xx=linspace(0,1,21);%将最大最小区间分成21个等分点(20等分),然后分别计算各个区间的个数
yy=hist(x,xx)/n/0.05;%计算各个区间的概率密度
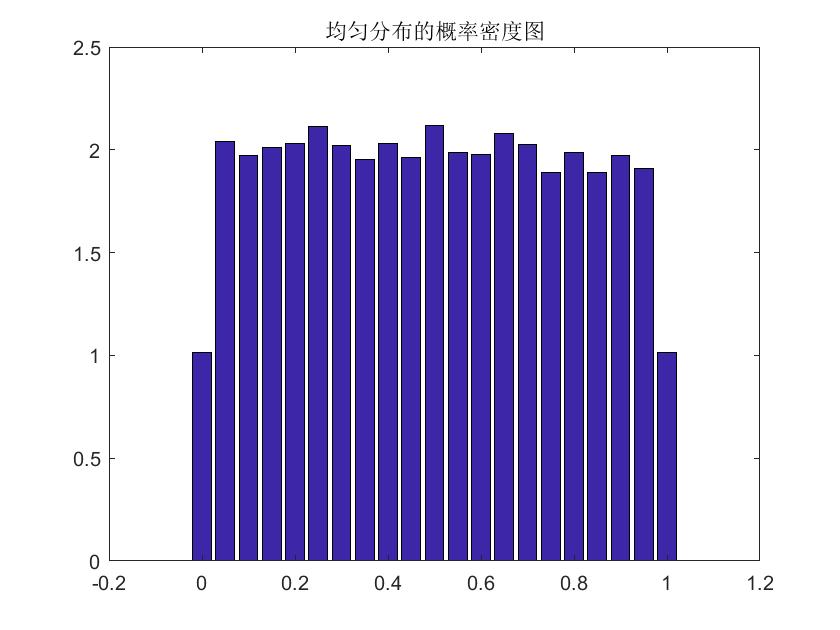
bar(xx,yy)%画出均匀分布的概率密度分布图
%%
y=2-sqrt(4-3*x);
yy2=hist(y,xx)/n/0.05;%计算各个区间的概率密度
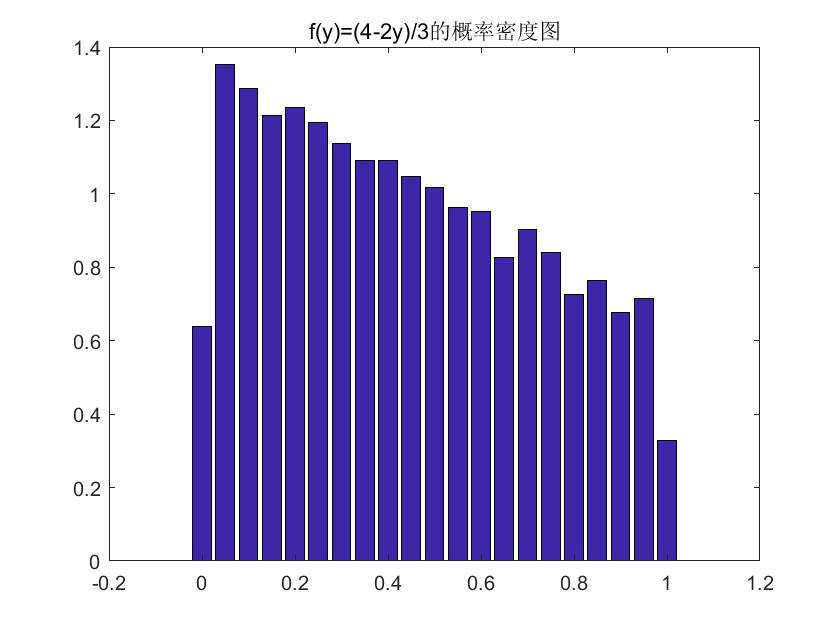
bar(xx,yy2)%画出特定分布概率密度分布图

更精彩的应用请参考：如何用带权重的蒙特卡洛计算积分？