如何用带权重的蒙特卡洛计算积分？

数值积分

有时会碰到一些难以表示成一般代数形式的积分，特别是在工程上，而且工程计算时一般也不需要精确的代数表达式，往往只要一定精度的数值结果。因此如何数值计算定积分呢？

为了便于比较，我们计算如下积分：

$${\int }_0^1\frac{1}{1+x^2}=\arctan x{|}_0^1=\frac{\pi }{4}\approx 0.7854$$ ### 均匀取点

%matlab code
clear;
x=linspace(0,1,200); %平均分成200个样本
y=1./(1+x.^2);
int=mean(y) %结果为0.7852
 

均匀取点在积分曲线比较平缓时，效果较好，如果有变化快的地方，需要单独做更加密集的取点，这个例子中曲线比较平缓，故精度相对较高。

均匀分布的蒙特卡洛取点

%matlab code
clear;
x=rand(1,200);%产生(0,1)区间均匀分布的200个随机数
y=1./(1+x.^2);
int2=mean(y)  %结果介于0.76~0.80
 

从效果上看，均匀分布的蒙特卡洛法不如均匀取点，会有涨落，精度不高，是否用更高精度的方法？观察图像$f(x)=\frac{1}{1+x^2}$:

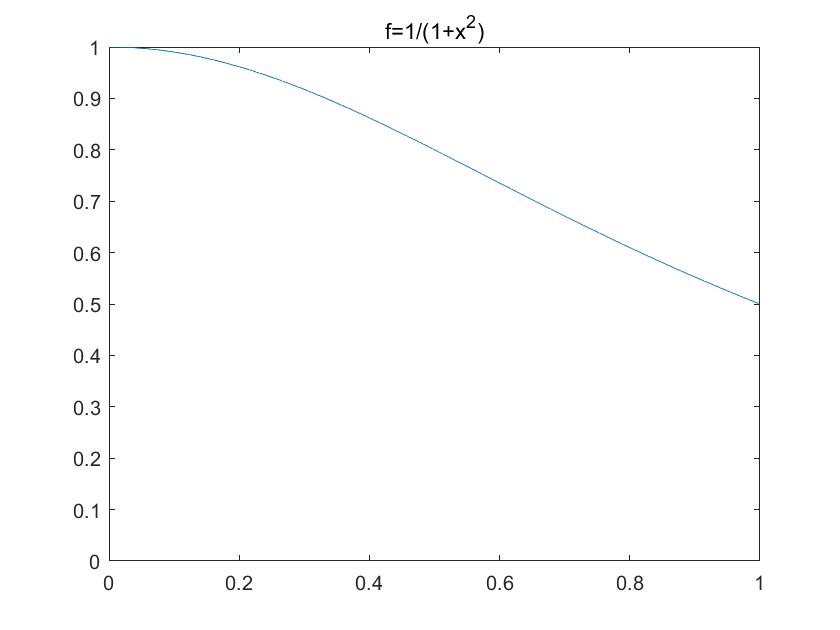
我们发现函数单调递减，那么我们在蒙特卡洛取点时，是否可以在x=0附近多取一些，x=1附近少取一些？比如我们按概率密度取点：

$$w=\frac{4}{3}(2-x)$$ 这个概率分布有以下特点：1、首先是一次函数，容易处理；2、x=0处和x=1处的概率比为2:1。最后由归一性可以确定系数。那么该如何产生这样的随机数呢？matlab有内置算法吗？请参看[Matlab如何用均匀分布产生其他分布？](https://www.jianshu.com/p/516e4fc4c7a4)

%matlab code
clear;
x=rand(1,200);
w=2-sqrt(4-3*x);
I=1./(1+w.^2)./(4-2*w)*3;
int3=mean(I)  %结果介于0.783~0.787
 

效果提高不少！可以猜想，如果我们选取的概率密度函数越接近原函数，那么蒙特卡洛的结果就越准确，但代价是求解反函数的过程会越复杂，需要折中。