经典二级运放设计
案例来自于《CMOS_analog Circuit Design》-Allen
一、基本构型
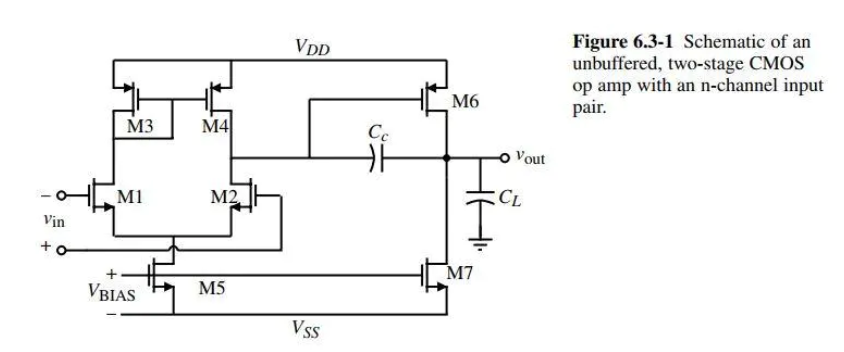
希望确定各晶体管的尺寸以达到如下要求:
| 基本参数 | 电平参数 | 频率参数 |
|---|---|---|
| $L=1\mu m $ | 共模电平$ICMR=-1 |
相位裕度60°,增益$A_v>5000$ |
| $C_L=10pF$ | $P_{diss} \leq 2mW$ | 压摆率$SR>10V/\mu s$ |
| $V_{DD}=-V_{SS}=2.5V$ | $V_{out} =\pm 2V$ | 带宽增益积$GB=5MHz$ |
另外器件参数$k_n'=110 \mu A/V^2,k_p'=50 \mu A/V^2,V_T=0.7\pm0.15V$。
二、设计过程:
(1) 满足相位裕度条件,确定米勒电容$C_c$
因为已知负载电容$C_L=10pF$,考虑到二级运放有一个隐含条件:第二级放大的跨导是第一级的10倍,即$g_{m6}=10~g_{m1}$,这样考虑零点后,要达到60°的裕度,第二极点要大于单位增益带宽$GB$的2.2倍(不考虑零点是$\sqrt{3}=1.73$倍)。根据这个条件可以确定$C_c$,它太小不能满足裕度要求,太大会衰减过快,不满足带宽要求。
$$ w_2 \geq 2.2GB \rightarrow \frac{g_{m6}}{C_L}\geq 2.2 \frac{g_{m1}}{C_c}\rightarrow C_c\geq 0.22C_L=2.2pF $$ 不妨取$C_c=3pF$。 #### (2)满足压摆率,确定偏置电流$I_5$ $$ SR=\frac{I_5}{C_c}\rightarrow I_5=SR\times C_c=30\mu A $$ #### (3)满足带宽增益积,确定$g_{m1},g_{m6}$ $$ \begin{aligned} g_{m1}&=GB\times C_c =(5\times10^6)(2\pi)(3\times10^{-12})=94.25\mu S\\ g_{m6}&=10 g_{m1}=942.5 \mu S \end{aligned} $$ ####(4) 满足输入共模电平,确定$(W/L)_{1,2},(W/L)_{3,4},(W/L)_5$ 由$M_1$的跨导可以很容易得到: $$ (W/L)_{1,2}=\frac{g_{m1}^2}{2k_n'I_1}=\frac{(94.25)^2}{2*110*15}=2.79\approx3 $$ 输入共模电平最大值为2V,要保证$M_3$管饱和,考虑到PMOS和NMOS阈值电压偏离的最坏情况,当$V_{T_n}=0.55,V_{T_p}=0.85$时,$M_3$的过驱电压最小,需要的宽长比最大,以保证最坏情况下也饱和。 $$ \begin{aligned} (W/L)_{3,4}&=\frac{2*0.5I_5}{k_p'(V_{DD}-V_{in_{max}}+V_{Tn_{min}}-V_{Tp_{max}})^2}\\ &=\frac{30\times10^{-6}}{50\times 10^{-6}(2.5-2+0.55-0.85)^2}=15 \end{aligned} $$ 输入共模电平最小为-1V,要保证$M_5$管饱和,考虑到NMOS阈值电压偏离的最坏情况,当$V_{T_n}=0.85$时,$M_5$的过驱电压最小,需要的宽长比最大,以保证最坏情况下也饱和。 $$ \begin{aligned} V_{ov5_{min}}&=V_{in_{min}}-V_{ss}-V_{Tn_{max}}-V_{ov1}\\ &=-1-(-2.5)-0.85-\sqrt{\frac{30\times10^{-6}}{110\times 10^{-6}\times3}}=0.35V\\ (W/L)_{5}&=\frac{2I_5}{k_n'V_{ov5_{min}}^2}=\frac{2(30\times10^{-6})}{110\times10^{-6}(0.35)^2}=4.49\approx4.5 \end{aligned} $$####(5)确定$(W/L)6,I_6,(W/L)7$ 有个很关键的一点,当共模输入时,$V{g6}=V{d4}=V_{d3}$,也就是三个PMOS管过驱电压一致,容易求出$g_{m4}=\sqrt{2I_4k_p'(W/L)4}=\sqrt{21550*15}=150\mu S$,结合$g{m6}=942.5\mu S,(W/L)_4=15$,可得:
$$ \begin{aligned} (W/L)_6&=(W/L)_4\times \frac{g_{m6}}{g_{m4}}\approx94\\ I_6&=I_4\times \frac{(W/L)_6}{(W/L)_4}\approx95\mu A\\ (W/L)_7&=(W/L)_5\times \frac{I_6}{I_5}\approx14 \end{aligned} $$ ####(6)检查输出电压、功耗、增益是否达标 $$ \begin{aligned} V_{ov6}&=\sqrt{2I_6/\beta_6}=\sqrt{2*95/(50*94)}\approx 0.2<0.5\\ V_{ov7}&=\sqrt{2I_7/\beta_7}=\sqrt{2*95/(110*14)}\approx 0.35<0.5\\ P_{diss}&=5*(30+95)=0.625<2mW\\ A_v&=A_{v1}*A_{V2}=(g_{m1}*r_{o1})(g_{m6}*r_{o6})\\ &=(\frac{94.25}{15*(0.04+0.05)})(\frac{942.5}{95*(0.04+0.05)})\\ &=69.8*110=7678>5000 \end{aligned} $$ ### 三、结果及半定量分析 输出的波动幅度时4V,$M_2$ 漏极波动约40mV($A_2\approx100$),输入两端相等时$V_{d2}=2.5-0.7-0.2=1.6V$,线性条件下,输入的最大差模电压约0.6mV($A_1\approx70$)。
四、Hspice 模拟结果
1、网表
* 二级运放Hspice 网表描述
*晶体管参数
M1 4 2 3 3 MN l=1u w=3u
M2 5 1 3 3 MN l=1u w=3u
M3 4 4 8 8 MP l=1u w=15u
M4 5 4 8 8 MP l=1u w=15u
M5 3 7 9 9 MN l=1u w=4.5u
M6 6 5 8 8 MP l=1u w=94u
M7 6 7 9 9 MN l=1u w=14u
M8 7 7 9 9 MN l=1u w=4.5u
Cc 6 5 3p
.model mn nmos level=1 vto=0.7 kp=110u lambda=0.04
.model mp pmos level=1 vto=-0.7 kp=50u lambda=0.05
*电源、输入及外部负载
Ibias 8 7 30u
VDD 8 0 2.5
VSS 9 0 -2.5
vin1 2 0 1 ac 1
vin2 1 0 1
CL 6 0 10p
*静态工作点
.op
*零极点
.pz v(6) vin1
*交流分析
.ac dec 10 1 100meg
.print ac v(6) vp(6)
.end
2、静态电压和晶体管参数如图:
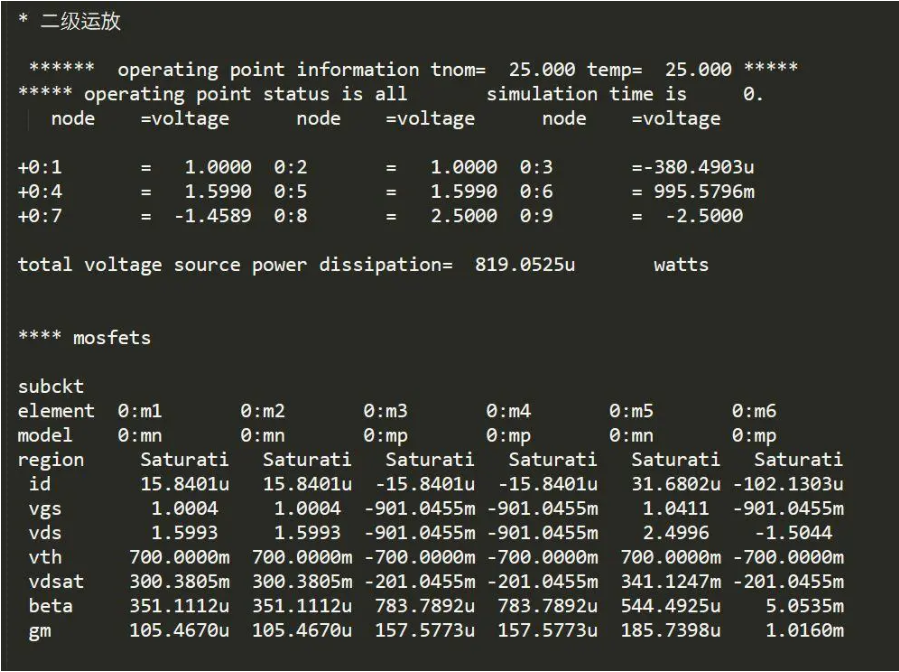
可以看出,管子都处于饱和状态,计算时忽略了沟道调制效应,实际的漏源电流会更大。因为NMOS的lambda小于PMOS,所以节点6处的电压大于0,为995.5796m。节点4的电压与之前分析一致,为1.6V。
3、零极点
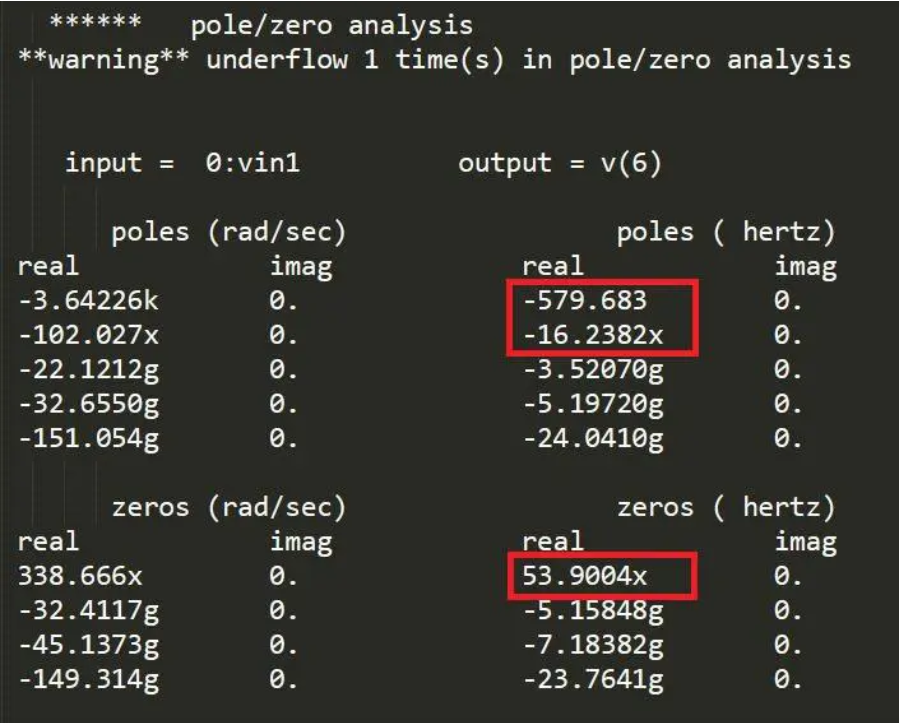
红框中是主要的极点和零点,单位是赫兹。单位增益带宽$GB=5MHz$,$p_2\approx 5*3=15MHz$,与16.2相近。主极点为$GB/A=651Hz$,与579相近。零点约为GB十倍,也相近。
4、波特图
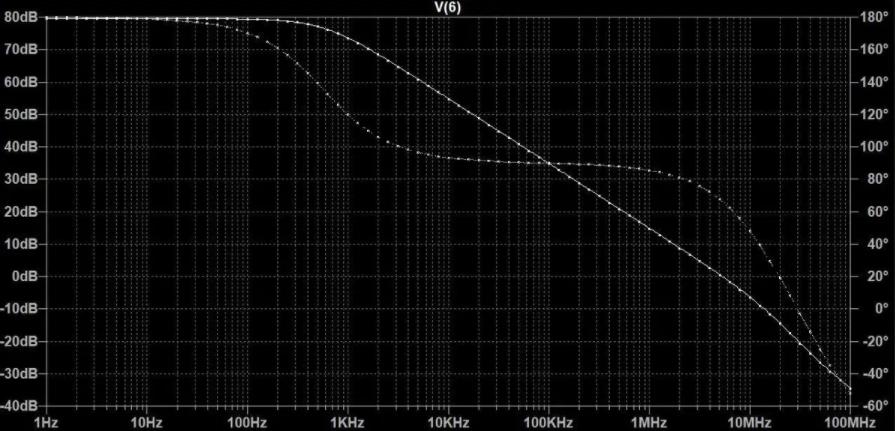
数据点显示单位带宽增益为5MHz,相位裕度为67.5°,还是比较符合预期的。