MDS降维实例展示

理论推导可以参看图像降维之MDS特征抽取方法 样例来自Multidimensional scaling

前言

MDS的理论推导已经有很多了，基本上来自周志华老师的西瓜书，但其中的细节还有许多不明白，因此希望通过matlab实例来理清所有脉络。

需要解释几点

1、输入数据

输入数据是距离矩阵D，而不是原始的m个d维向量，说明有数据的信息量缺失，但它们的相对位置关系是明确的。实例中的距离矩阵如下：

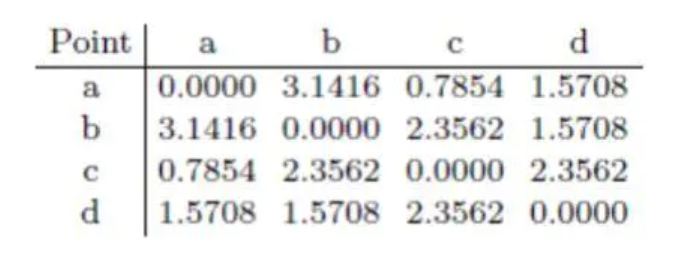
也就是有4组数据，但它们的维度不知道，姑且认为较大吧，我们的任务是找4组二维的数据$Z_{4\times 2}$，让它们间的距离和上述距离相等。

2、计算Z的内积矩阵

通过两者距离相等的关系，我们希望可以求出Z的内积矩阵$B=ZZ^T$的各个元素(这里和西瓜书不一样，因为这里的Z由行向量组成，每行表示一组数据)，具体的公式有点复杂：

$$ b_{ij}=-\frac{1}{2}(distt^2_{ij}-distt^2{i.}-distt^2{.j}+dist^2) $$ 但幸运的是，这都是纸老虎，在matlab具体计算的时候，其实各部分很简单，详见后面**matal代码部分**。 #### 3、由内积矩阵获得Z 因为$B_{m\times m}$是是对称阵，可以得到m个特征值和特征向量(这里西瓜书写的是原数据的维度d，应该是不对的)，特征向量从大到小排序： $$ B=V \Lambda V^T=V \Lambda ^{1/2} (V\Lambda ^{1/2})^T=ZZ^T $$ 所以$Z_{m\times m}=V\Lambda^{1/2}$。 为了实现降维，我们提取前d'个特征值和特征向量，即:$V_*=V_{m\times d'}$，$\Lambda_*=\Lambda_{d'\times d'}$。得到 $Z_{m\times d'}=V_*\Lambda_*^{1/2}$

matlab代码

clear;clc;
%输入的欧式距离对称矩阵
D=[0 3.1416 0.7854 1.5708;3.1416 0 2.3562 1.5708;
   0.7854 2.3562 0 2.3562;1.5708 1.5708 2.3562 0];
%距离平方对称阵
D2=D.*D; %每个元素为distt(ij)^2
%获得B矩阵
distt2i=mean(D2);    %对列求平均1*4矩阵
distt2j=mean(D2,2);  %对行求平均4*1矩阵
dist2=mean(mean(D2));      %所有距离的平均1*1矩阵
%matlab可以自动展开成4*4矩阵并做加减计算
B=-1/2*(D2-distt2i-distt2j+dist2);
%B=VAV'
[V,A]=eig(B);
%翻转特征向量，从特征值大到小排序
V=fliplr(V);A=wrev(diag(A));
%% 提取前两个最大的特征值，和特征向量，计算Z，实现降维
Z=V(:,1:2)*diag(sqrt(A(1:2)))

结果如下：

Z剔除了部分信息后，内积矩阵与B是有差距的，但总体可以接受，最后再比较Z的4组样本间的两两距离：

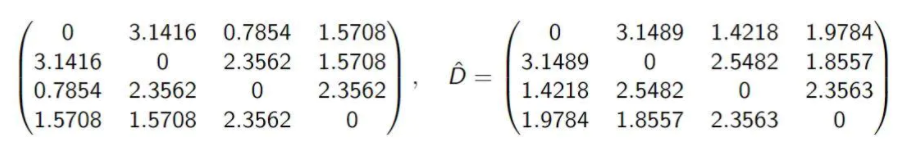
可以看出，整体效果还是很好的！

小结

• 内积矩阵B的维度是$m\times m$，m为样本数量，求取得特征值和特征向量也有m个，不是d个(原样本的维度)。
• 降维是通过选取前d'个特征值，和对应d'个特征列向量，获得$Z_{m\times d'}$。