奈奎斯特准则和香农公式的半定量解释

一、问题引出

通信原理中介绍信道容量时，经常会碰到两个公式：奈奎斯特准则和香农公式。前者在理想情况，后者在有噪声情况下。它们看起来很像，但始终没想到一个直观的方式联系在一起。为什么带宽越大就能传输越多信号？香农公式如何推导的？

虽然网上有很多解释，但多停留在应用层面，我希望了解这些公式到底时如何来的，花了很多时间找资料并思考，终于有了一个比较清晰的图像，希望和大家共勉。

二、奈奎斯特准则

奈奎斯特(Nyquist)推导出理想低通信道下的最高码元传输速率为：

$$ B_{max}=2W $$ 信息最高传输速率为： $$ C_{max}=B_{max}\times \log_2(M)=2W\log_2(M) $$ W理想低通的带宽，M为信号电平进制数，最简单的例子是码元只有0，1两个状态，一个码元包含1bit信息量。也可以是码元电平信号通过DA转换(数模转换器)成0，1/4，1/2，3/4四种电平，那么一个码元包含的信息量就是$\log_2 (4)=2 bit$。

但我们知道高频电磁波可以通过解调将频谱搬移到低通区。以GSM为例，它的某一个中心频率是890.2MHz，他的频率范围是[890.1,890.3]MHz，中间共200kHz，这就是W带宽，即频谱宽度。

用奈奎斯特准则可以计算，GSM这个频段的最高码元速率为:$B_{max}=2\times 200k=4\times 10^5Baud$ ,如果电平进制数为4，则理想信道容量为$C_{max}=B_{max}\times \log_2(4)=8\times 10^5b/s$。

奈奎斯特准则半定量解释

那么这到底为什么是这样呢？如果拥有200kHz的带宽，我们具体如何发送码元(电平信号)才能达到最大传输速率呢？这个问题也困扰了自己很久，网上的解答一般是用采样定理搪塞过去，思考了很久，终于有了答案。

假设我们要发送1/4码元的很窄脉冲，该脉冲在频域上是很宽的($\delta(t)$做傅里叶变换为1，分布整个频段)，但我们这里有200kHz的频带限制，所以相当于窄脉冲再通过一个200kHz的低通滤波器，这样信号在时域会展宽，数学形式是sinc函数：

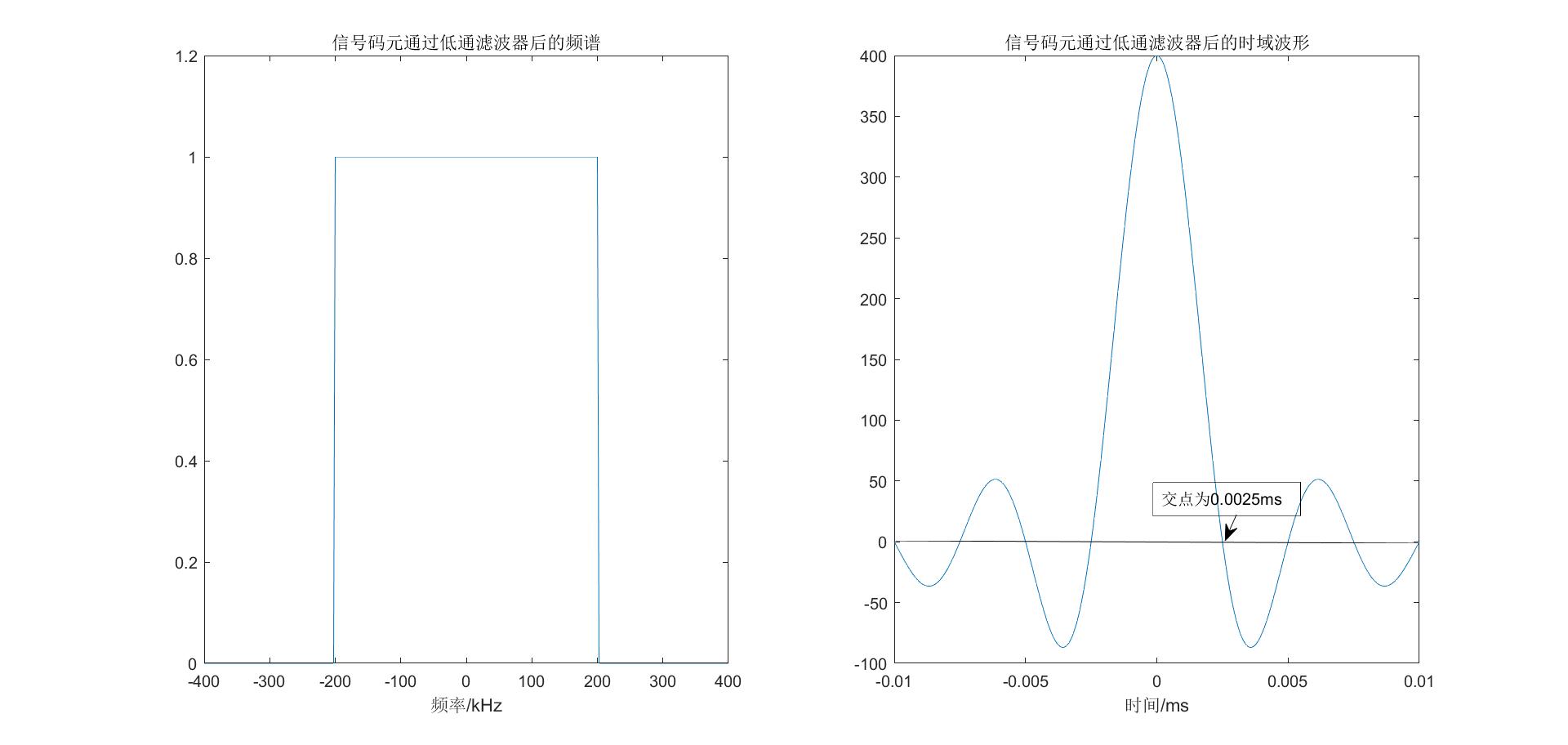
也就是说我们发送一系列码元的时域波形是右图形态在不同时间上的叠加，如果发送码元的时间过于靠近，比如小于1/2W=1/400k=0.0025ms，那么两个尖峰会发生混叠，造成信号失真。因此，码元的发送需要一定间隔，间隔时间是1/2W，也就是最高转输速率为$B_{max}=2W$，这是由有限带宽决定的，如果带宽越大，则传输码元的信号会越尖锐，信号越容易分辨，两信号间隔时间可以越短，码元传输速率就越快。

5G通信之所以能够比4G快10倍，也是这个原因。4G的中心频段约2000MHz，频谱偏移1%的带宽资源为20M([1990,2010]MHz)，5G的商用中心频率为28GHz，频谱偏移1%的带宽资源为280M。也就是5G发送的信号码元的峰值更尖锐，码元间的时间间隔更短，每秒传输的码元更多，速率自然更快。

三、香农公式

高斯白噪声干扰的信道中，信息传输的速率最大是：

$$ C_{max}=W\log_2(1+S/N) $$ W是信道带宽，S是信源的平均功率，N是信道内高斯噪声功率。对比奈奎斯特公式，两者都有带宽，都有log，但是该怎么联系在一起呢？

香农公式的半定量解释

假设信源的电平信号为$V_S$，平均功率为S，信道噪声电平为$V_N$，平均功率N，接收电平信号为$V_T$，平均功率为P。因为噪声信号和信源信号不相关，可以得到：

$$ P=S+N \rightarrow V_T^2=V_S^2+V_N^2 $$ 接下来是很关键一步，接收到的电平最大电平为1V，信道存在1/16V大小的随机噪声电压，那么我们最多可以把信号分“多细”才不至于被信号干扰呢，如果分0，1两个电平，那么1/16的噪声电压显然不会干扰信号。如果信号分成32份，那么噪声相对于1/32就足够大，以至于我们不能分清1/32V的电压是0电压干扰后的结果(这里的干扰电压是平均值)，还是2/32电压干扰后的结果，所以直观上看，我们最多只能将信号分成16份，也就是M=16，这样由奈奎斯特准则可以计算最大信道容量$C_{max}=2W\log_2(16)=8W$。

更加一般的结论就是，信号平均电平为$V_T$，干扰平均电平为$V_N$时，信号的进制数M最大为：

$$ M_{max}=V_T/V_N=\sqrt{V_T^2/V_N^2}=\sqrt{1+V_S^2/V_N^2}=\sqrt{ 1+S/N} $$ 带入奈奎斯特公式有： $$ C_{max}=2W\log_2(M)=W\log_2(1+S/N) $$ 就是香农公式！中间有一些不严谨的地方，但其直观图像就是那么简单。

可以看出，噪声限制了信号不能分“太细”，否则会被噪声淹没，不可分辨。

四、总结

奈奎斯特准则和香农公式实际上是从带宽和噪声两个方面来描述其对信道容量的影响。如果带宽无限，无噪声，那么码元可以非常高频得发送，码元可以分成非常细，单个码元能描述的信息量可以趋于无穷。

但是现实上，带宽是有限的，码元发送的间隔被带宽限制了，其发送速率有上限，这就是奈奎斯特准则。其次，信道肯定是有噪声的，进制数不可能无限细分，最细只能是噪声电压的量级，每个码元携带的信息量也是有上限的，这可以导出香农公式。

参考资料

Shannon's Equation 《深入浅出理解通信原理》 《信号与系统》第二版 奥本海姆