电磁波在柱坐标和球坐标下的本征解

一、背景

课程和习题中，我们通常接触的都是平面电磁波，但现实生活中却常常碰到柱面波和球面波，如通电导线辐射场、手机信号等。而且工程上，平面波也可以按柱面波和球面波展开。

那么电磁波在柱坐标和球坐标下的本征解是什么样的形式呢？什么样的波源可以产生这样的电磁场呢？这就是本文要讨论的问题。

二、真空中的时谐场

首先列出真空中的麦克斯韦方程：

$$ \begin{cases} \nabla \cdot \vec{E}=0 \\ \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \\ \nabla \cdot \vec{B}=0 \\ \nabla \times \vec{B} =\frac{1}{c^2} \frac{\partial \vec{E}}{\partial t} \\ \end{cases} $$ 分别表示空间中无电荷，法拉第电磁感应定律，无磁单极子，安培定律。第四项对时间求导可得： $$ \frac{1}{c^2} \frac{\partial ^2\vec{E}}{\partial t^2} = \nabla \times \frac{\partial \vec{B}}{\partial t} = \nabla \times (-\nabla \times \vec{E})=-[\nabla(\nabla \cdot \vec{E})-\nabla ^2 \vec{E}]=\nabla ^2 \vec{E} $$ 第三步用到了矢量微分的运算公式，可以用直角坐标展开来证明，过程比较繁琐。

在考虑时谐场，即$\vec{E}=\vec{E}(x,y,z)e^{-i \omega t}$，带入上式可得到：

$$ \nabla ^2 \vec{E}+k^2\vec{E}=0 $$ $k \equiv \omega /c$这就得到了亥姆霍兹方程。可以容易得到直角坐标系下本征解： $$ \vec{E}=C \cdot e^{i(ky-\omega t)} \hat{z} $$ 

三、柱坐标下的本征解

亥姆霍兹方程求解的一个难点是，Laplace算符作用的是带有方向的矢量，直角坐标系下，基矢方向不变，但柱坐标和球坐标下，基矢也会随求导改变。

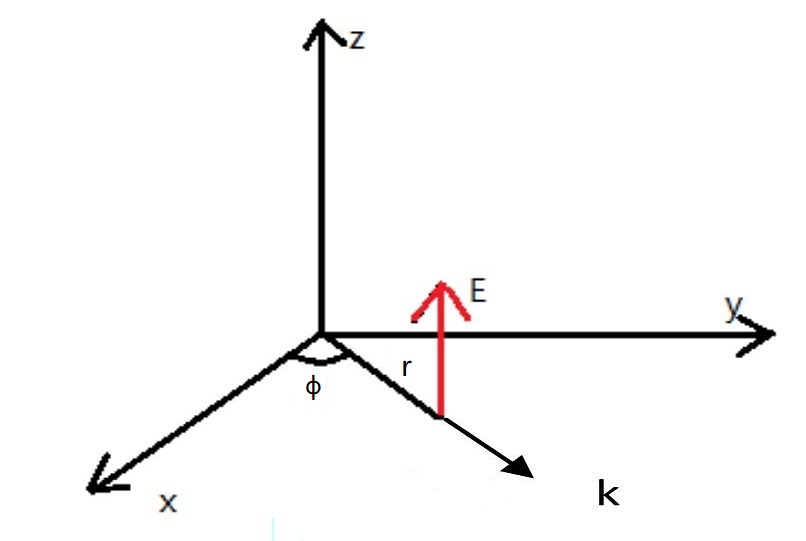
为了计算简单，假设波矢方向$\vec{k}$沿$\hat{r}$方向，电场方向沿$z$轴，大小只与$r,\phi$有关，与$z$无关。即$\vec{E}=E(r,\phi)\hat{z}$，参考附录中的矢量微分公式可得：

$$ \nabla ^2 \vec{E}=(\nabla ^2 \vec{E})_z=\nabla ^2 E_z \hat{z}=\nabla ^2 E(r,\phi) \hat{z}=[\frac{1}{r} \frac{\partial}{\partial r}(r\frac{\partial E}{\partial r})+\frac{1}{r^2} \frac{\partial^2 E}{\partial \phi^2}+\frac{\partial^2 E}{\partial z^2}]\hat{z}\\ =(\frac{\partial^2 E}{\partial r^2}+\frac{1}{r}\frac{\partial E}{\partial r}+\frac{1}{r^2} \frac{\partial^2 E}{\partial \phi^2})\hat{z} $$ 带入亥姆霍兹方程，消去方向$\hat{z}$得： $$ \frac{\partial^2 E}{\partial r^2}+\frac{1}{r}\frac{\partial E}{\partial r}+\frac{1}{r^2} \frac{\partial^2 E}{\partial \phi^2}+k^2E=0 $$ 这个方程需要用分离变量法求解：$E=R\cdot\Psi$ $$ \begin{cases} \frac{ d^2\Psi}{d\phi^2}+m^2 \Psi=0 \\ \frac{d^2 R}{dr^2}+\frac{1}{r}\frac{d R}{d r}+(k^2-\frac{m^2}{r^2})R=0 \\ \end{cases} $$ 解得： $$ E=H_m(kr)[A\cos(m\phi)+B\sin(m\phi)] $$ 这里R满足的方程是贝塞尔方程，不同的m可以解出不同的表达式，一般的求解方法是多项式待定系数法，解起来非常繁琐，姑且用一个整体表示它即$H_m(kr)$称为汉克函数，它包含实部和虚部： $$ H_m(kr)=J_m(kr)+iN_m(kr) $$ $J_m(kr)$为贝塞尔函数，$N_m(kr)$为诺伊曼函数，定性上只要知道这两个函数在方向上震荡衰减，衰减的振幅正比于$\frac {1}{\sqrt{r}}$，即$\vec{E}$在较远处(大于一个波长就有相当好的近似)可简化为： $$ \vec{E}=[A\cos(m\phi)+B\sin(m\phi)]H_m(kr)e^{-i\omega t}\hat{z}\approx A'\sin(m\phi+B')\frac{1}{\sqrt{kr}}e^{i(kr-\omega t)}\hat{z} $$ 我们可以看出，电场的大小绕着z轴(沿$\phi$方向)周期震荡，沿着r方向呈现$\frac {1}{\sqrt{r}}$ 递减，相位关系与平面波类似$e^{i(kr-\omega t)}$。电场大小随$\frac {1}{\sqrt{r}}$ 递减也反映了能流守恒，因为单位高度的同轴椭圆的侧面积S正比于r，单位时间流出单位侧面积的能量正比于$E^2\varpropto 1/r$，因此单位高度的同轴椭圆总能量流出守恒。

四、球坐标下的本征解

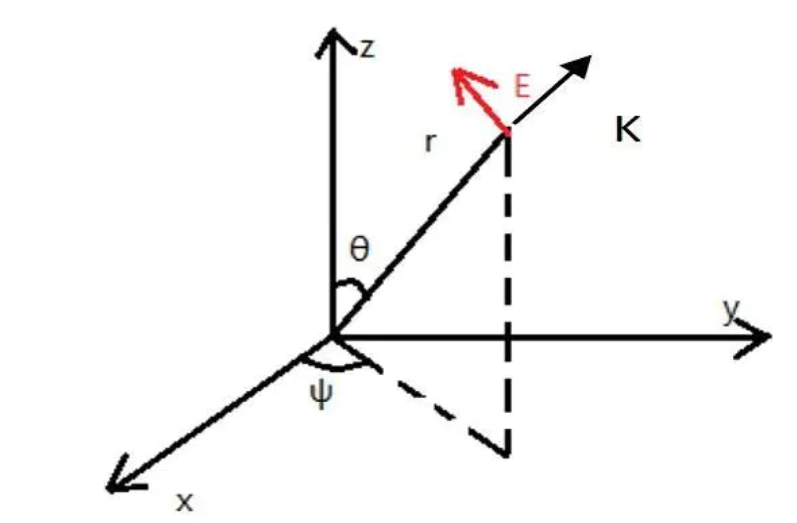
为了简化问题，假设波矢$\vec{k}$的方向沿$\hat{r}$，电场的大小只与$r,\theta$有关，而与$\psi$无关，即$\vec{E}=E(r,\theta)\hat{\theta}$，参考附录中的矢量微分公式可得：

$$ \nabla ^2 \vec{E}=(\nabla ^2 \vec{E})_{\theta}=\nabla ^2 E_{\theta} \hat{\theta}+\frac{2}{r^2}[0-\frac{E_{\theta}}{2\sin^2\theta}+0]\hat{\theta}\\ =[\frac{\partial^2 E}{\partial r^2}+\frac{2}{r}\frac{\partial E}{\partial r}+\frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta}(\sin \theta \frac{ \partial E}{\partial \theta})-\frac{1}{r^2\sin^2 \theta}E]\hat{\theta} $$ 带入亥姆霍兹方程，消去方向$\hat{\theta}$得： $$ \frac{\partial^2 E}{\partial r^2}+\frac{2}{r}\frac{\partial E}{\partial r}+\frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta}(\sin \theta \frac{ \partial E}{\partial \theta})-\frac{1}{r^2\sin^2 \theta}E+k^2E=0 $$ 用分离变量法求解：$E=R\cdot\Theta$ $$ \begin{cases} \frac{1}{ \sin \theta} \frac{d }{d \theta}(\sin \theta \frac{ d \Theta}{d \theta})-\frac{1}{\sin^2 \theta}\Theta+l(l+1)\Theta=0 \\ \frac{d^2 R}{dr^2}+\frac{2}{r}\frac{d R}{d r}+[k^2-\frac{l(l+1)}{r^2}]R=0 \\ \end{cases} $$ 解得： $$ E=C\cdot h_l(kr)P_l(\cos \theta) $$ 其中$C$为常数，$P_l(\cos \theta)$是$\Theta$所满足方程的解，它是$l$阶$m=1$的关联勒让德函数，这个函数在解氢原子波函数的时候也会用到。径向的方程$R$满足球贝塞尔方程，其解$h_l(kr)$是球汉克函数： $$ h_l(kr)=j_l(kr)+in_l(kr) $$ $j_l(kr)$表示$l$阶的球贝塞尔函数，$n_l(kr)$表示$l$阶的球诺伊曼函数，与柱坐标系的结果类似，我们只需要知道这个表达式在较远处的行为： $$ \vec{E}= C\cdot P_l(\cos \theta)h_l(kr)e^{-i\omega t}\hat{\theta} \approx C \cdot P_l(\cos \theta)\frac{1}{kr}e^{i(kr-\omega t)}\hat{\theta}\varpropto \frac{1}{r}e^{i(kr-\omega t)}\hat{\theta} $$ 因此可以定性看出，电场的方向沿$\hat{\theta}$，幅度与$\psi$无关，随$\theta$变化，随$1/r$递减，电磁波整体的方向沿$\hat{r}$传播。

振幅呈$1/r$衰减也反应了能量守恒，因为球面的面积正比于$r^2$，球面上单位面积流出的能量正比于$E^2 \varpropto 1/r^2$，因此半径为$r$的球面流出的能量是守恒的。

Tip:

求解亥姆霍兹方程时要利用拉普拉斯算符$\nabla ^2$，与作用于不带方向的标量(如氢原子波函数)相比，当它作用于带方向的电场时，会多出几项(查看附录的矢量微分公式)，这是因为这里的“方向”也是会随坐标改变的，求偏导时会多出因方向变化导致的添加项。

五、本征解对应的波源可能是什么？

现在我们已经清楚了电场波在直角坐标、柱坐标和球坐标下的本征解，假设空间中真的有这种波存在，那么它的波源是什么呢？总不可能凭空产生电磁场吧？

我们先列出这些波在基态的形式： 平面波：$\vec{E}=C \cdot e^{i(ky-\omega t)} \hat{z}$ 柱面波：$\vec{E}=H_0(kr)e^{-i\omega t}\hat{z}\approx C'\frac{e^{i(kr-\omega t)}}{\sqrt{kr}}\hat{z}$($m=0$) 球面波：$\vec{E}= P_0(\cos \theta)h_0(kr)e^{-i\omega t}\hat{\theta} \approx C' \sin \theta \frac{e^{i(kr-\omega t)}}{kr}\hat{\theta}$($l=0$)

由空间对称性可以猜想，平面波是由无限大平面的震荡电流产生的；柱面波是由无限长导线的震荡电流产生的；而球面波的形式就是偶极子。下面具体推导验证这些波源产生的波是否和本征解一致。

1、无限大平面的电流源

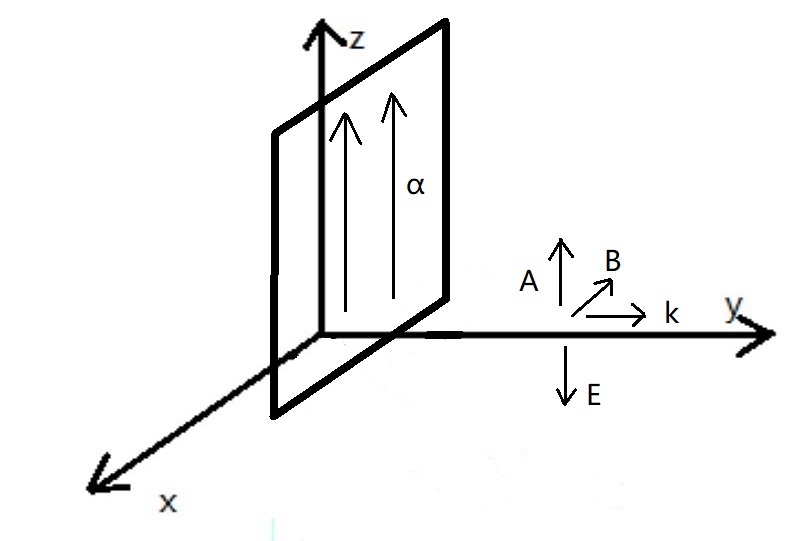
如图，无限大平面在oxz平面上，电流线密度$\alpha=\alpha_0 e^{-i\omega t}$，现在计算(0,y,0)处的电场强度，为此需要先求磁矢势$\vec{A}$，再对其求旋度得到磁场强度$\vec{B}$，最后再求电场强度$\vec{E}$，oxz平面上，距离远点$l=\sqrt{x^2+z^2}$处的一小段电流为$\alpha_0 dx \cdot dz$，因为它会随时间变化，因此该点到(0,y,0)处的相位延时为$k\sqrt{y^2+l^2}$，可以得到磁矢势的积分形式：

$$ \vec{A}=\frac{\mu_0}{4\pi}\int\frac{\alpha_0 e^{-i(\omega t-k\sqrt{y^2+l^2})}dxdz}{\sqrt{y^2+l^2}}\hat{z} $$ x、z的平面积分转为极坐标积分，因为小段电流的相位和大小与角度无关，可直接积分： $$ \vec{A}=\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\int_0^{\infty}\frac{e^{i k\sqrt{y^2+l^2}}ldl}{\sqrt{y^2+l^2}}\hat{z} $$ 对e指数泰勒展开可得： $$ \vec{A}=\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\int_0^{\infty}\sum_{n=0}^\infty \frac{({i k\sqrt{y^2+l^2}}) ^n}{n!\sqrt{y^2+l^2}}\frac{1}{2} dl^2\hat{z} $$ 将$l^2$看作积分变量，分别对各项积分得： $$ \vec{A}=\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\sum_{n=0}^\infty \frac{({i k}) ^n}{(n+1)!}[(y^2+L^2)^{\frac{n+1}{2}}-y^{n+1}]\hat{z} $$ 这里的$L$应该趋于无穷大，这样会导致$|A|$发散，这是因为磁矢势的大小与零势点的位置有关系，对磁矢势求旋度可以消除零势点位置的影响，我们可以先求出磁场，然后再对L取无穷： $$ \vec{B}=\nabla\times \vec{A}=\frac{\partial A}{\partial y} \hat{x}=\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\sum_{n=0}^\infty \frac{({i k}) ^n}{(n+1)!}[\frac{(n+1)}{2}(y^2+L^2)^ {\frac{n-1}{2}}2y-(n+1)y^{n}]\hat{x} $$ 将求和级数凑成指数，容易得到： $$ \vec{B}=\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\sum_{n=0}^\infty[\frac{(ik\sqrt{y^2+L^2})^n}{n!}\frac{y}{\sqrt{y^2+L^2}}-\frac{(iky)^n}{n!}]\hat{x}=-\frac{\mu_0\alpha_0}{2}e^{i(ky-\omega t)}\hat{x}+\frac{\mu_0\alpha_0}{2}e^{-i\omega t}\frac{e^{ik\sqrt{y^2+L^2}}y}{\sqrt{y^2+L^2}} \hat{x} $$ 容易知道，第二项在$L\rightarrow \infty$时为0，因此最后结果为： $$ \vec{B}=-\frac{\mu_0\alpha_0}{2}e^{i(ky-\omega t)}\hat{x} $$ 又可求出电场： $$ \vec{E}=-\frac{w\hat{k}}{k}\times\vec{B}=-\frac{\mu_0\alpha_0c}{2}e^{i(ky-\omega t)}\hat{z} $$ 这和平面波的表达式一致。

2、无限长导线电流源

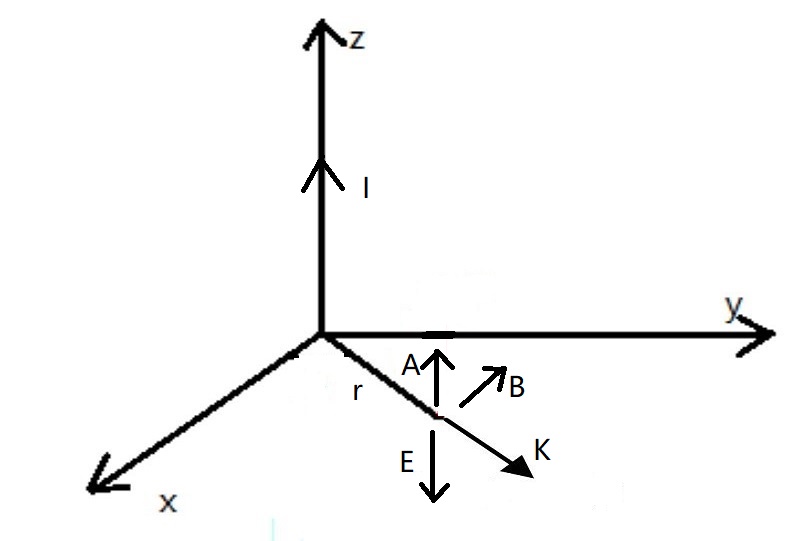假设在z轴上有变化的电流，$I=I_0e^{-i\omega t}$。接下来求解，oxy平面内，离原点r处的磁矢势$\vec{A}$。同样要考虑不同位置处小段电流对r处的相位不同：

$$ \vec{A}=\frac{\mu_0I_0}{4\pi}e^{-i\omega t}\int_{-\infty}^{\infty}\frac{e^{ik\sqrt{r^2+l^2}}dl}{\sqrt{r^2+l^2}}\hat{z} $$ 这个积分很难处理，先求电场表达式： $$ \vec{E}=-\frac{\partial\vec{A}}{\partial t}=-\frac{\mu_0I_0\omega}{4\pi}e^{-i\omega t}(-i) \int_{-\infty}^{\infty}\frac{e^{ik\sqrt{r^2+l^2}}dl}{\sqrt{r^2+l^2}}\hat{z} $$ 对比上一节柱坐标系下的本征解形式，只能先猜想积分项就是m=0时的汉克函数，实际上，我在一本参考书的课后习题上发现确实有这种关系(奚定平.贝塞尔函数.北京：高等教育出版社，1999) 

我们需要用欧拉公式展开指数项，得到：

$$ \begin{cases} \int_{-\infty}^\infty \frac{ \cos(k \sqrt{r^2+l^2})}{\sqrt{r^2+l^2}}dl= -\pi N_0(kr)\\ i\int_{-\infty}^\infty \frac{ \sin(k \sqrt{r^2+l^2})}{\sqrt{r^2+l^2}}dl=i\pi J_0(kr) \end{cases} $$ 因此电场可化为： $$ \vec{E}=-\frac{\partial\vec{A}}{\partial t}=-\frac{\mu_0I_0\omega}{4\pi}e^{-i\omega t}(-i) [-\pi N_0(kr)+i \pi J_0(kr)]\hat{z}=-\frac{\mu_0I_0\omega}{4}e^{-i\omega t} [J_0(kr)+i N_0(kr)]\hat{z} $$ 为了保险起见，我们可以用数值的方式验证上述积分是否正确：(matlab里面有现成的贝塞尔和诺伊曼函数) 

六、软件模拟

最后，为了验证这种源确实可以产生对应的电磁波，我打算用电磁波软件comsol3.5模拟。

1、平面波

初始条件及环境：

下图是无限长空腔的俯视图：

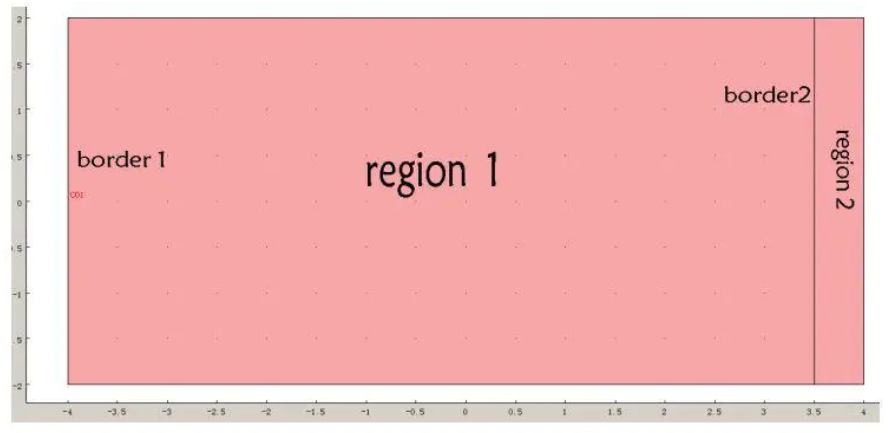
尺寸及模块：长X宽=8mX4m，RF模式下的TE模式； region 1 为真空；region 2为PML系数物质； border 1：垂直于纸面的面电流源$\alpha=1·e^{-i\omega t} A$，频率$f=2\pi /\omega=0.5G Hz$，及波长$\lambda=0.6m$ border 2: 连续边界条件，即磁场平行分量相等：$\vec{n}\times(\vec{H_1}-\vec{H_2})=0$

仿真结果：

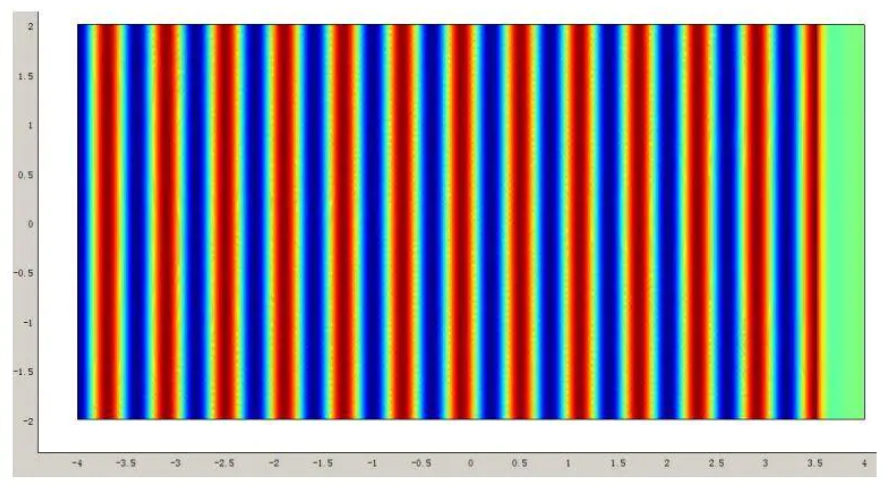颜色表示电磁场的值，红色为正，蓝色为负。容易看出，无限大平面电流产生的确实是平面波，波长为0.6m。

选取y=0处的数据点磁场强度$H-x$进一步验证：

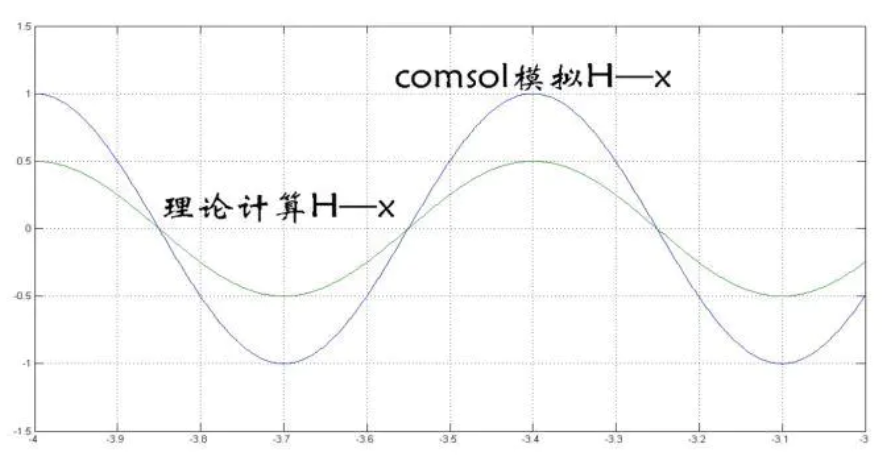
重新推导磁场强度，带入数值可以得到：

$$ \vec{H}=(\frac {\alpha_0}{2})e^{i(kx-\omega t)}\hat{y}= \frac {1}{2}\cos(kx)\hat{y} $$ 这里令$t=0$，取实部，可以发现理论计算比实际小一半，什么原因呢？

因为理论计算时考虑了波向y的正方向和负方向两边扩散，而模拟时相当于负方向的波和正方向叠加，因此会有二倍的效果。

二、柱面波

下图是无限长圆柱的俯视图：

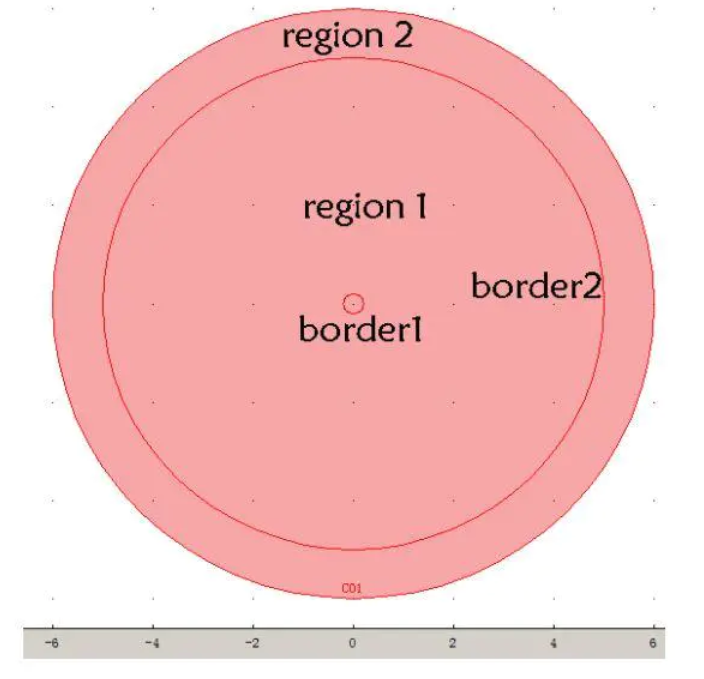
尺寸及模块：三个园半径分别为0.2、5、6m，RF模式下的TE模式； region 1 为真空；region 2为PML系数物质； border 1：垂直于纸面的面电流源$I=2\pi r \alpha · e^{-i\omega t} A=1e^{-i\omega t}$，频率$f=2\pi /\omega=0.5G Hz$，或波长$\lambda=0.6m$ border 2: 连续边界条件。 其他边界条件：PEC完美电导体，即电场无垂直分量$E_z=0$;

值得注意的是，这里的电流源是有一定粗细的导线，这和理论推导时的假设不一样，仿真结果会在数值上于理论不一致，但仍然是贝塞尔函数。

模拟结果：

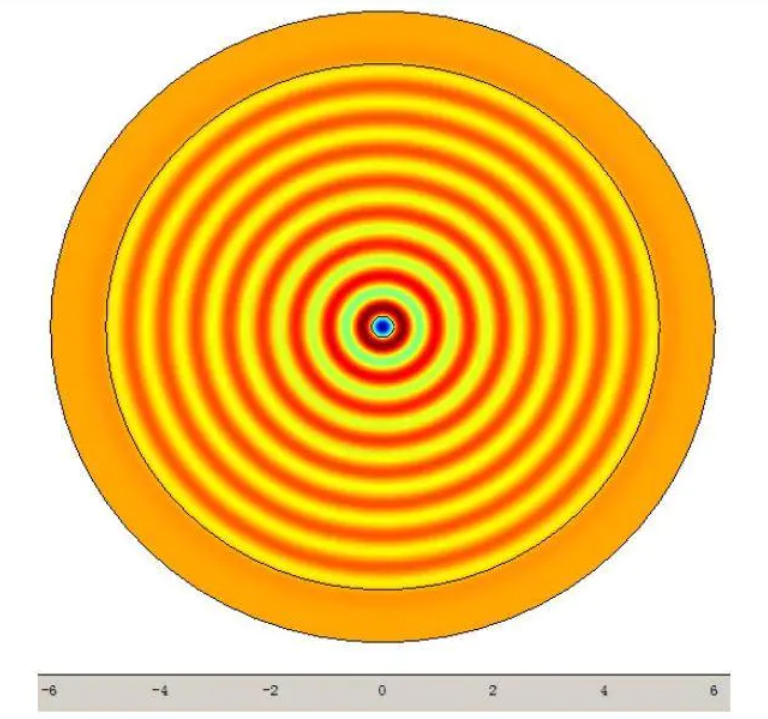初步可以看出这是柱面波，波长接近0.6m。

选取y=0的半径上获取数据，做出电场随半径变化图$E-r$：

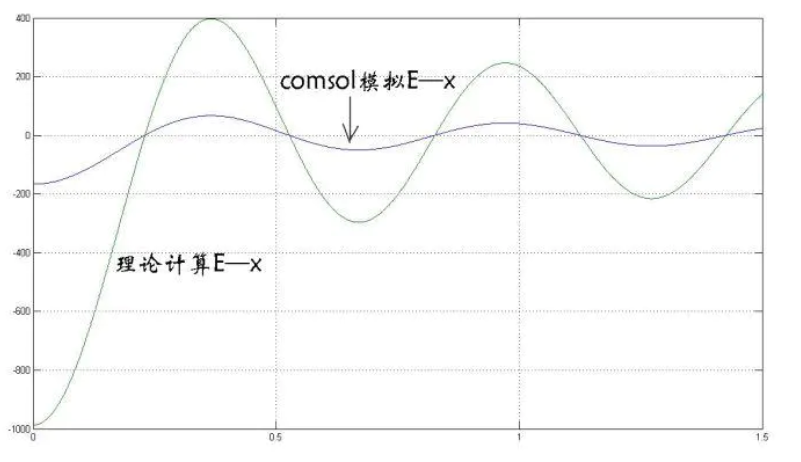
将数据带入理论表达式有：(t=0，取实部)

$$ \vec{E}=-\frac{\mu_0I_0\omega}{4}e^{-i\omega t} [J_0(kr)+i N_0(kr)]\hat{z}=-987J_0(kr)\hat{z} $$ 两者为什么会不一样呢？这就是源的问题：如果把comsol模拟的源"0.2m的圈"改成点源，可以得到与理论一致的结果。

总结

• 拉普拉斯算符对矢量的作用不同于标量，前者还要考虑不同坐标系下单位矢量随位置的变化。
• 平面波的波源是无限大平面的震荡电流（二维电流），柱面波的波源是无线长导线的震荡电流（一维波源），球面波的波源是偶极震荡（零维电流）。
• 虽然不会证明，还是列出零阶贝塞尔函数和诺伊曼函数的积分表达式：

$$ \begin{cases} N_0(r)=-\frac{1}{\pi}\int_{-\infty}^\infty \frac{\cos(\sqrt{r^2+l^2})}{\sqrt{r^2+l^2}}dl\\ J_0(r)=\frac{1}{\pi}\int_{-\infty}^\infty \frac{ \sin( \sqrt{r^2+l^2})}{\sqrt{r^2+l^2}}dl \end{cases} $$ - 仿真模拟需要在数值上考虑更多细节，对理论的理解会更深一层。 ## 附录：