随机失调误差推导
一、随机失调误差的结论
Sansen《精粹》的15章失配中,直接给出了米勒放大器的随机失配和系统失配电压的公式,还给出了共模抑制比和随机失配电压的风骚关系:
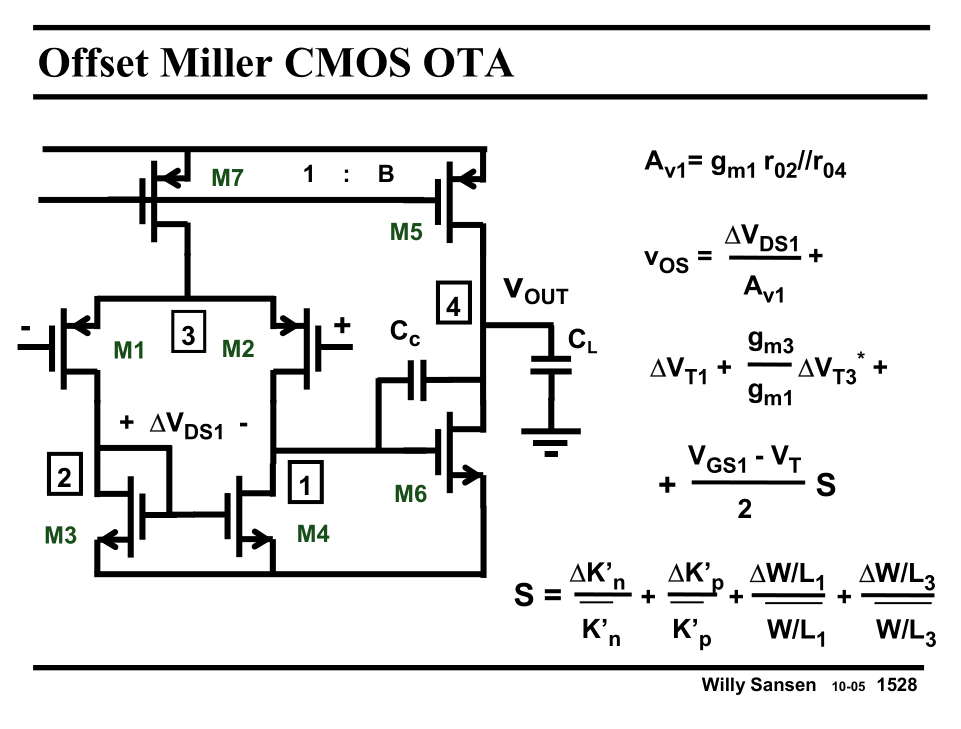
二、随机失调电压$V_{osr}$的推导
随机失调电压是差分信号$V_{osr}$为了平衡工艺偏差导致的随机失配k'、W/L、$V_{th}$得到的。随机失配会造成两边电流不相等,由此产生输出的漂移:
$$ V_{osr}g_{m2}r_{o2}//r_{o4}=(\Delta I_{ds2} +\Delta I_{ds4})r_{o2}//r_{o4} \tag {1} $$ $$ \frac{\Delta I_{ds2}}{I_{ds2}}=\frac{\Delta k'_2}{k'_2}+\frac{\Delta (W/L)_2}{(W/L)_2}+\frac{\Delta V_{th2}}{V_{gt2}/2}\tag {2} $$ $$ \frac{\Delta I_{ds4}}{I_{ds4}}=\frac{\Delta k'_4}{k'_4}+\frac{\Delta (W/L)_4}{(W/L)_4}+\frac{\Delta V_{th4}}{V_{gt4}/2}\tag {3} $$由$I_{ds4}=I_{ds2}=2g_{m2}v_{gt2}=2g_{m4}v_{gt4}$,将(2)(3)带入(1)得:
$$ \begin{aligned} &V_{osr}g_{m2}=I_{ds2}(\frac{\Delta k'_2}{k'_2}+\frac{\Delta (W/L)_2}{(W/L)_2}+\frac{\Delta V_{th2}}{V_{gt2}/2}+\frac{\Delta k'_4}{k'_4}+\frac{\Delta (W/L)_4}{(W/L)_4}+\frac{\Delta V_{th4}}{V_{gt4}/2})\\ &V_{osr}=\Delta V_{th2}+\Delta V_{th4}\frac{V_{gt2}}{V_{gt4}}+\frac{V_{gt2}}{2}(\frac{\Delta k'_2}{k'_2}+\frac{\Delta (W/L)_2}{(W/L)_2}+\frac{\Delta k'_4}{k'_4}+\frac{\Delta (W/L)_4}{(W/L)_4})\\ &V_{osr}=\Delta V_{th2}+\Delta V_{th4}\frac{g_{m4}}{g_{m2}}+\frac{V_{gt2}}{2}(\frac{\Delta k'_2}{k'_2}+\frac{\Delta (W/L)_2}{(W/L)_2}+\frac{\Delta k'_4}{k'_4}+\frac{\Delta (W/L)_4}{(W/L)_4}) \end{aligned} $$与书上的结论一致。
三、随机共模抑制比$CMRR_r$的推导
随机共模抑制比可以用定义推导,但计算共模增益的时候,要用到上面的结论,很巧妙地将静态的失调电压和动态的共模增益联系在一起:
$$ A_{dd}=g_{m2}r_{o2}//r_{o4} $$ $$ \begin{aligned} A_{dc}&=\frac{dI_{ds4}-dI_{ds3}}{dV_{inc}}r_{o2}//r_{o4}\\ &=\frac{dI_{ds4}}{dV_{inc}}\frac{dI_{ds4}-dI_{ds3}}{dI_{ds4}}r_{o2}//r_{o4}\\ &=\frac{1}{2R_B}\frac{V_{osr}g_{m2}}{I_{ds4}}r_{o2}//r_{o4} \end{aligned} $$ 第二步和第三步相当巧妙。 $$ CMRR_r=\frac{A_{dd}}{A_{dc}}=\frac{2R_B I_{ds_4}}{V_{osr}}=\frac{R_B I_{B}}{V_{osr}}=\frac{V_E L_E}{V_{osr}}\approx \frac{10}{V_{osr}} $$