围观Razavi和Sansen打架——电流并联反馈

一、排兵布阵

Sansen出招

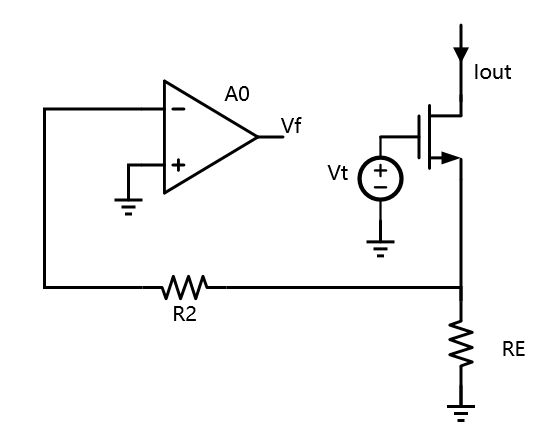
Sansen《模集精粹》第14章反馈中介绍电流并联反馈时，要求输入电阻，和输出电阻，他的结果是：

$$ R_{in}=\frac{R_2+R_E//\frac{1}{g_m}}{1+LG}\approx \frac{R_2}{A_0}（负载短路） $$ $$ R_{out}=r_0(1+g_mR_E)(1+LG)\approx r_og_mR_EA_0（负载开路） $$ 这里假设了mos管的$g_m$很大。

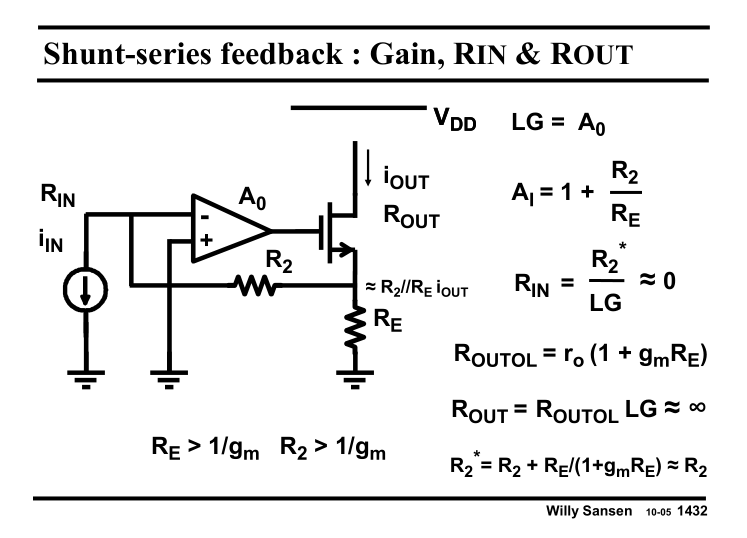
Razavi出招

Razavi第八章的反馈也有这样的案例，同样是电流并联反馈。 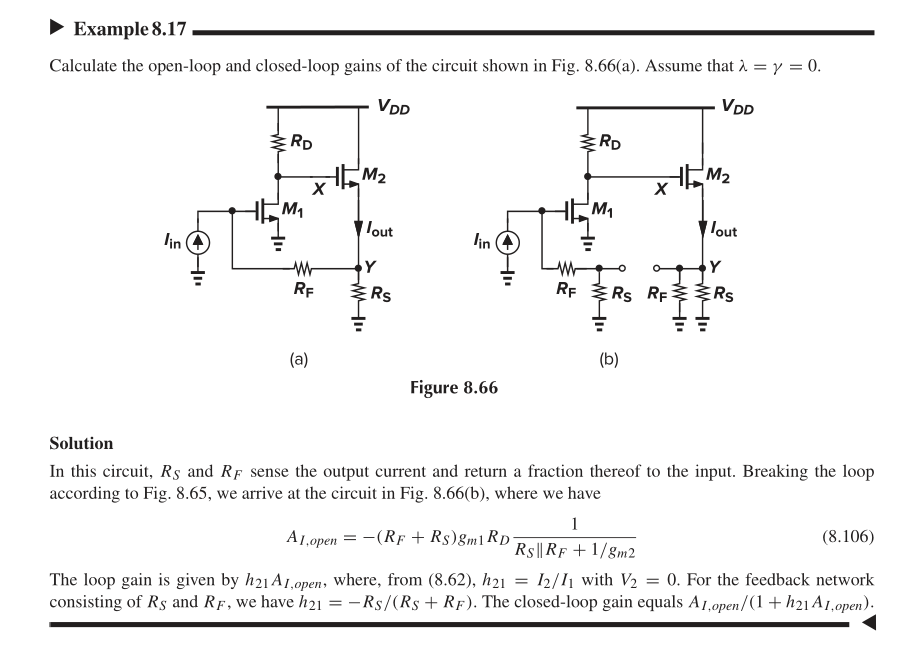用Razavi计算的结果是：

$$ R_{in}=\frac{R_2+R_E}{1+LG}\approx \frac{R_2+R_E}{A_0}（负载开路） $$ $$ R_{out}=r_0(1+g_mR_E//R_2)(1+LG)\approx r_og_mR_E//R_2A_0（负载短路） $$

求输入输出的时候，采用二端口网络的方法，确实需要向拉扎维一样，输入开路，输出短路。但为什么Sansen要输入短路，输出开路呢？而且两者的结果不一样。电路就摆在那里，仿真也只有一个结果，到底哪位大佬的结果正确呢？

二、格雷劝架

不得不说，格雷的《Analysis and Design of Analog Integrated Circuits》确实是经典中的经典，配套的课后习题解答更是自学利器！第八章除了详细介绍了二端口的计算方法，还介绍了Return Ratio的方法。更加给力的是，课后习题用两种方法手算了电压并联反馈的增益、输入输出电阻。

经过格雷的拨乱反正，发现两位大佬都没有错，因为两个人用了不同的方法，两种方法定义的环路增益、输入、输出电阻的求法都不一样。

Sansen用的是Return Ratio的方法，计算负载时需要用Blackman公式，而不是用二端口的开路负载乘上或除以环路增益。

Razavi用的是二端口的方法，该方法定义的环路增益与Return Ratio不同。

三、Razavi的二端口方法

1、打开环路

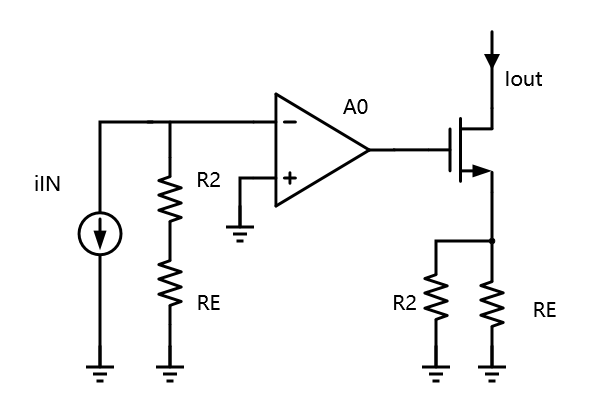
2、分别计算开环增益$A_{open}$，反馈系数$F$

$$ A_{open}=\frac{I_{out}}{I_{in}}=(R_2+R_E)A_0\frac{g_m}{1+g_mR_2//R_E}\approx\frac{(R_2+R_E)^2}{R_2R_E}A_0 $$ $$ F=\frac{I_F}{I_{out}}=\frac{I_F}{(1+R_2/R_E)I_F}=\frac{R_E}{R_E+R_2} $$ 由此可以得到环路增益： $$ AF=\frac{R_2+R_E}{R_2}A_0 $$ 这里得到的环路增益和Sansen中的不同，结果相差一个系数$\frac{R_2+R_E}{R_2}$，但都可以得到最终闭环$R_{in}，R_{out}$的结果。

3、计算输入电阻、输出电阻

$$ R_{in_{close}}=\frac{R_{in_{open}}}{1+AF}=\frac{R_2+R_E}{1+A_0\frac{R_2+R_E}{R_2}}\approx\frac{R_2}{A_0} $$ $$ R_{out_{close}}=R_{out_{open}}(1+AF)=r_o(1+g_mR_2//R_E)(1+A_0\frac{R_2+R_E}{R_2})\approx r_og_mR_EA_0 $$

四、Sansen的Return Ratio方法

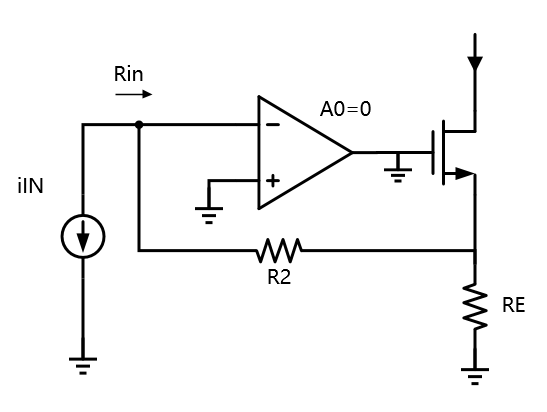
1、断开环路，输入置零，求环路增益LG

$$ LG=\frac{V_f}{V_t}=A_0 $$ 这里假设$g_m$很大，nmos表现为跟随器。 ### 2、输入输出负载 Return Ratio的方法需要用Blackman公式计算输入输出负载： $$ Z_{port}=Z_{port}(k=0)[\frac{1+R(port\_shorted)}{1+R(port\_open)}] $$ #### 输出负载 简单来说，如果要求输出负载：需要将环路中的放大器增益置为0(即k=0)，此时NMOS的栅极相当于接地。输入端的电流置零，计算此时的输出电阻$R_{outol}=r_o(1+g_mR_E)$。  $R(port\_shorted)$是将输出短路，恢复放大器增益时的环路增益；$R(port\_open)$是将输出开路，恢复放大器增益时的环路增益；两者的比值通常都是LG或者1/LG，具体要看反馈的类型。这里是输出是电流反馈，负载会提高，因此要乘以(1+LG)。 $$ R_{out}=R_{outol}(1+LG)\approx r_og_mR_EA_0 $$ 与Razavi的结果一致

输入负载

同样的道理，计算输入电阻的时候，将放大器增益置零(即k=0)，得到$R_{inol}=R_2+R_E//\frac{1}{g_m}\approx R_2$。

最后输入电阻：

$$ R_{in}=\frac{R_{inol}}{1+LG}\approx \frac{R_2}{A_0} $$ 这也和Razavi的结果一致。

五、总结

反馈的精确计算一直是模大中的一大难点，比较常用的方法是二端口法：

• 断开环路求$A_{open}$(需考虑负载)
• 计算环路增益$A_{open}F$
• 计算闭环增益，输入电阻，输出电阻

另一种方法是Return Ratio的方法：

• 输入置零，断开环路，加测试信号求环路增益LG(特别注意这里的环路增益和二端口的环路增益定义不同)
• Blackman 公式计算输入输出电阻

当环路中的放大器不理想($R_{in}\ne \infty,R_{out}\ne 0,A_0\ne \infty$)，比较格雷大佬的习题计算结果，发现二端口的方法会准确一些。

向Razavi，Sansen，格雷三位大佬致敬！