差分电路的噪声分析

之前一直对差分电路的噪声分析存在恐惧，特来整理一波。

求下图差分电路中三个mos管对差模输出的热噪声$\overline{dV_{out}^2}$，且假设mos管的$\lambda=\gamma=0$。

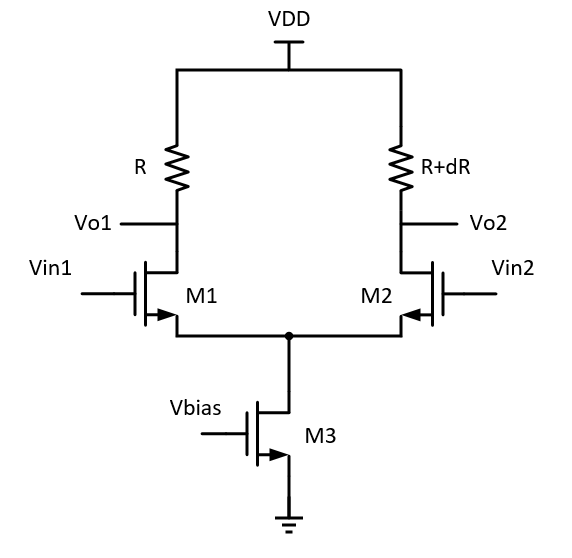
由于两个输入端的噪声不相关，因此不能用源极虚地的方式求输入到输出的增益（虽然最后结果确实一样）。

1、M1、2对输出噪声

先考虑M1管的热噪声，其噪声等效到栅极为：
$$
\overline{dV_{n1}^2}=\frac{4kT \gamma}{g_{m1}}
$$
下面用小信号模型计算该输入对两个差模输出的增益：

列KCL方程可得：
$$
\begin{cases}
\frac{V_{o1}}{R}+(V_{in1}-V_s)g_{m1}=0 \\
(V_{in1}-V_s)g_{m1}= V_s g_{m2} \\
\frac{V_{o2}}{R}=V_s g_{m2}
\end{cases}
$$
由$g_{m1}=g_{m2}=g_m$解得：
$$
V_{o1}=-\frac{g_mR}{2} V_{in1}\\
V_{o2}= \frac{g_mR}{2} V_{in1}
$$
因此M1对输出的噪声贡献：
$$
\overline{dV_{oM1}^2}=\frac{4kT \gamma}{g_{m1}}(g_mR)^2=4kT \gamma g_{m}R^2
$$

由对称性可以知道，M2对输出的噪声也是：
$$
\overline{dV_{oM2}^2}=4kT \gamma g_{m}R^2
$$

2、M3对输出噪声

M3为尾电流管，在电路对称的情况下，其对输出的增益为0，也就是说两边的噪声是相关的，会互相抵消，但是电路的负载电阻存在失配，因此会产生小的增益变化：
$$
A_3=\frac{V_{o2}-V_{o1}}{V_3}=\frac{V_3g_{m3}\frac{1}{2}\Delta R}{V_3}=\frac{1}{2}g_{m3}\Delta R
$$
所以M3对输出的噪声贡献：
$$
\overline{dV_{oM3}^2}=\frac{4kT \gamma}{g_{m3}}(\frac{1}{2}g_{m3}\Delta R)^2=kT \gamma g_{m3}\Delta R^2
$$

因此总输出噪声：
$$
\overline{dV_{out}^2}=\overline{dV_{oM1}^2}+\overline{dV_{oM2}^2}+\overline{dV_{oM3}^2}\\
=8kT\gamma g_m R^2+kT\gamma g_{m3}\Delta R^2
$$