Differences between four kinds of IIR filters(A)
摘要：本文研究了低通、高通、带通、带阻模拟滤波器和数字滤波器的频率响应特性，单位脉冲响应以及零极点分布图，并定性解释了零极点分布图与频率响应特性的关系。
1.Analog Filters
a.Low Pass
$$H(s)=\frac {2.232}{s^3+2.614s^2+3.416s+2.232} $$$w_p=0.4\pi ; w_s=0.6\pi;A_p=3dB;A_s=10dB;$
b.High Pass
$$H(s)=\frac {s^3}{s^3+3.625s^2+6.569s+5.953} $$$w_p=0.6\pi ; w_s=0.4\pi;A_p=3dB;A_s=10dB;$
c.Band Pass
$$H(s)=\frac {0.4196s^2}{s^4+0.9161s^3+5.157s^2+2.17s+5.611} $$$w_{p_1}=0.4\pi ;w_{p_2}=0.6\pi; w_{s_1}=0.3\pi;w_{s_2}=0.7\pi;A_p=3dB;A_s=10dB;$
d.Band Stop
$$H(s)=\frac {s^4+4.737s^2+5.611}{s^4+1.539s^3+5.922s^2+3.646s+5.611} $$$w_{p_1}=0.3\pi ;w_{p_2}=0.7\pi; w_{s_1}=0.4\pi;w_{s_2}=0.6\pi;A_p=3dB;A_s=10dB;$
Discussion
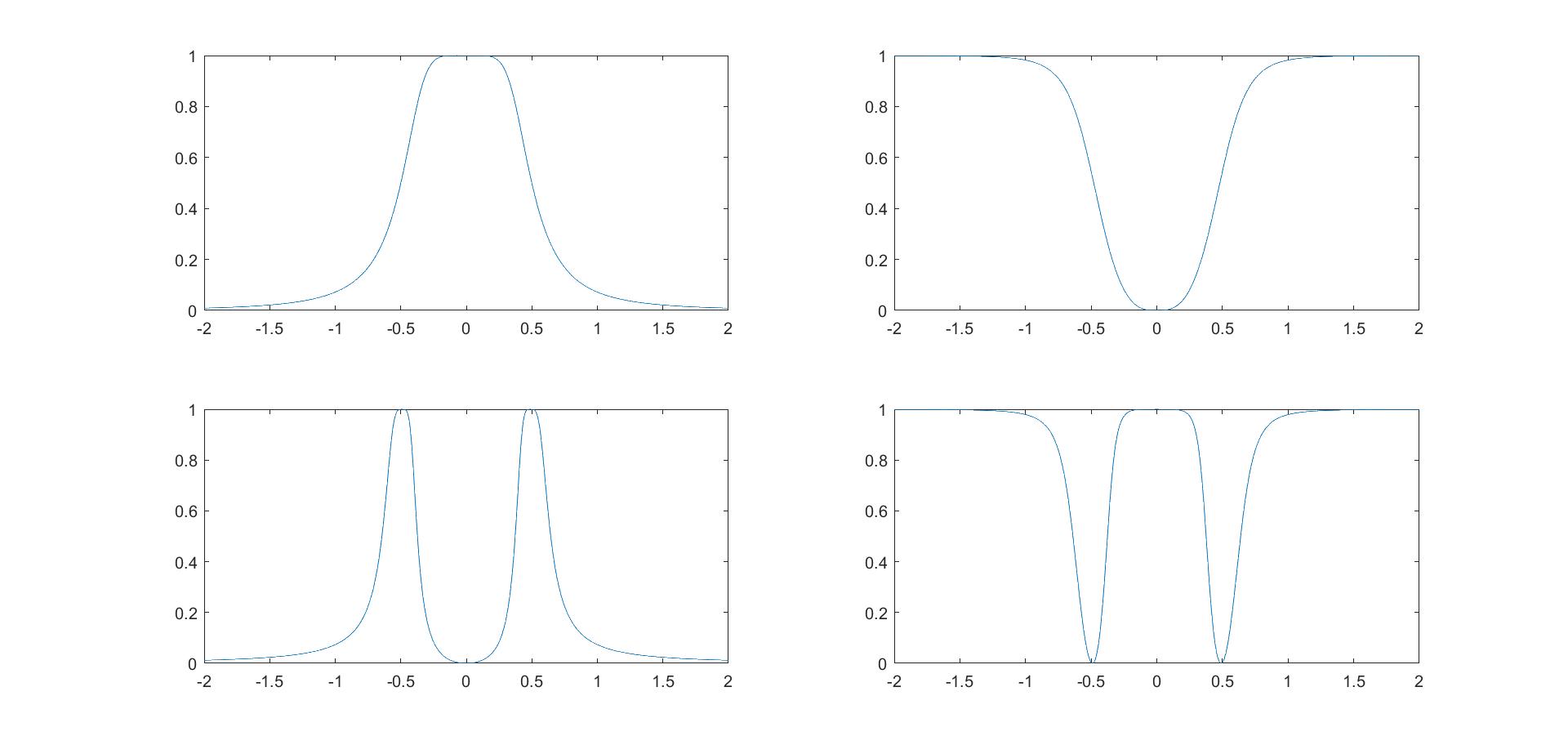
（1）比较四个模拟滤波器的频率响应$|H(j\omega)|$，$\omega\subseteq[-2\pi,2\pi]$，横坐标坐标归一化$\pi$。
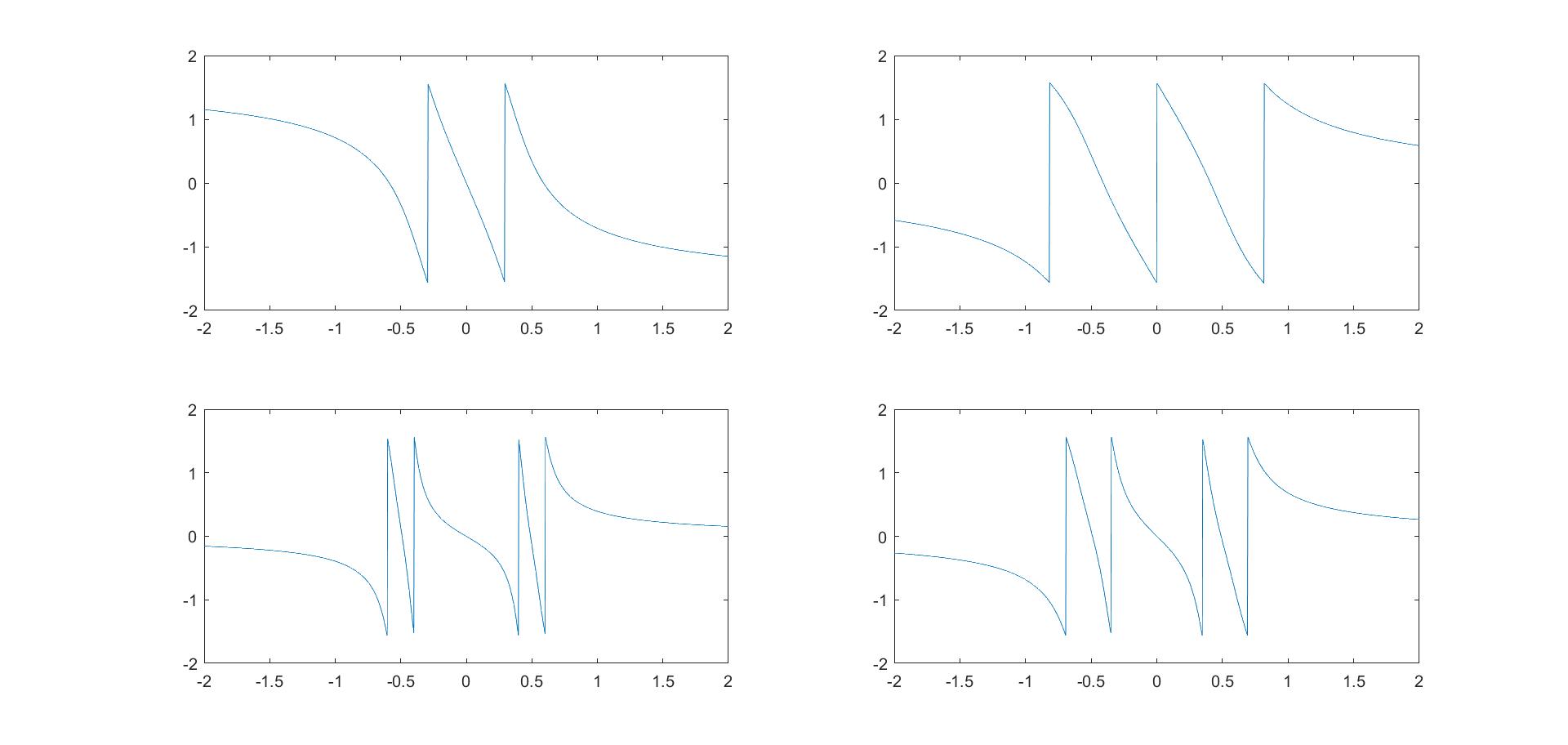
（2）比较四个模拟滤波器的相位响应$\psi(j\omega)$
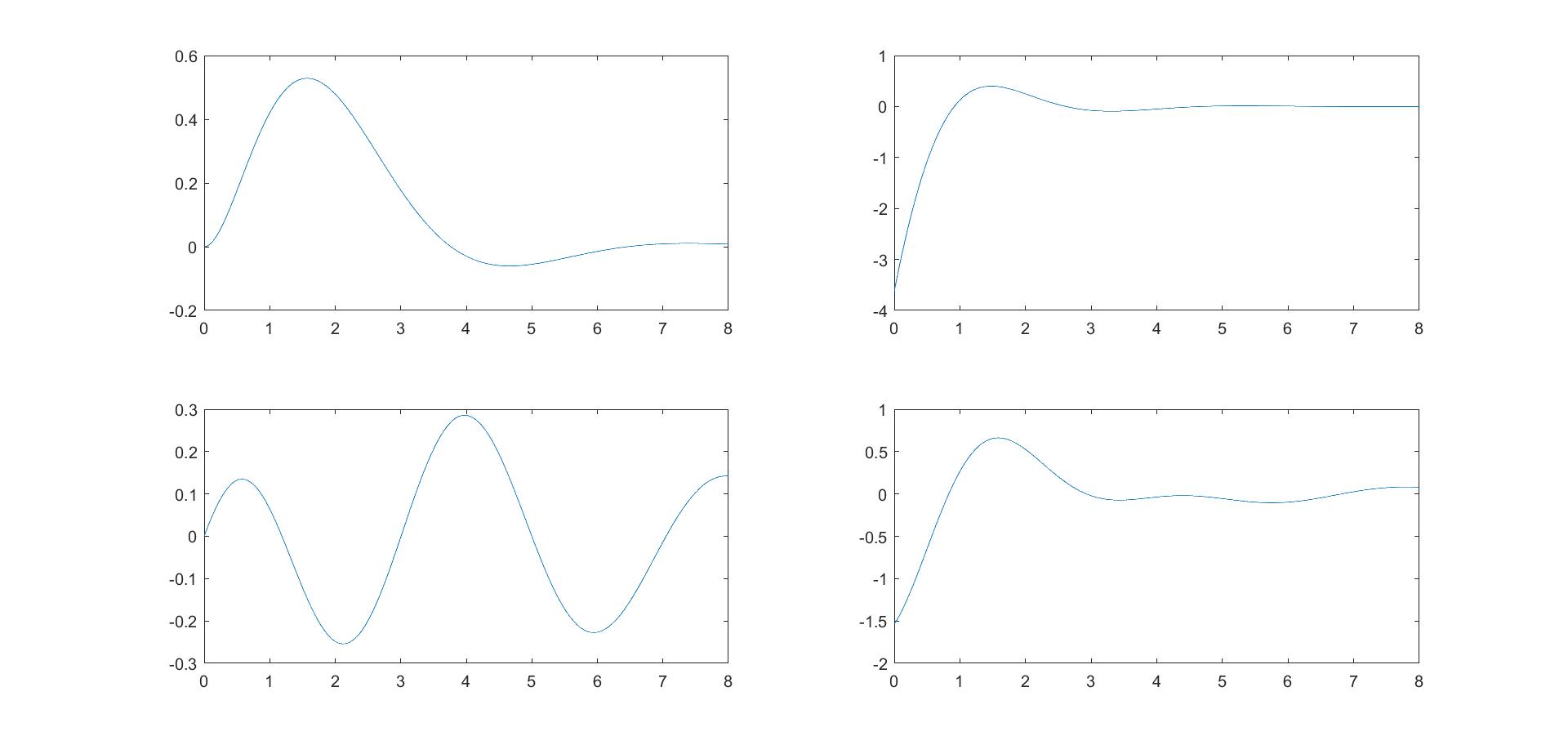
（3）比较四个模拟滤波器的单位脉冲响应$h(t)$
（4）比较四个模拟滤波器的零极点分布图
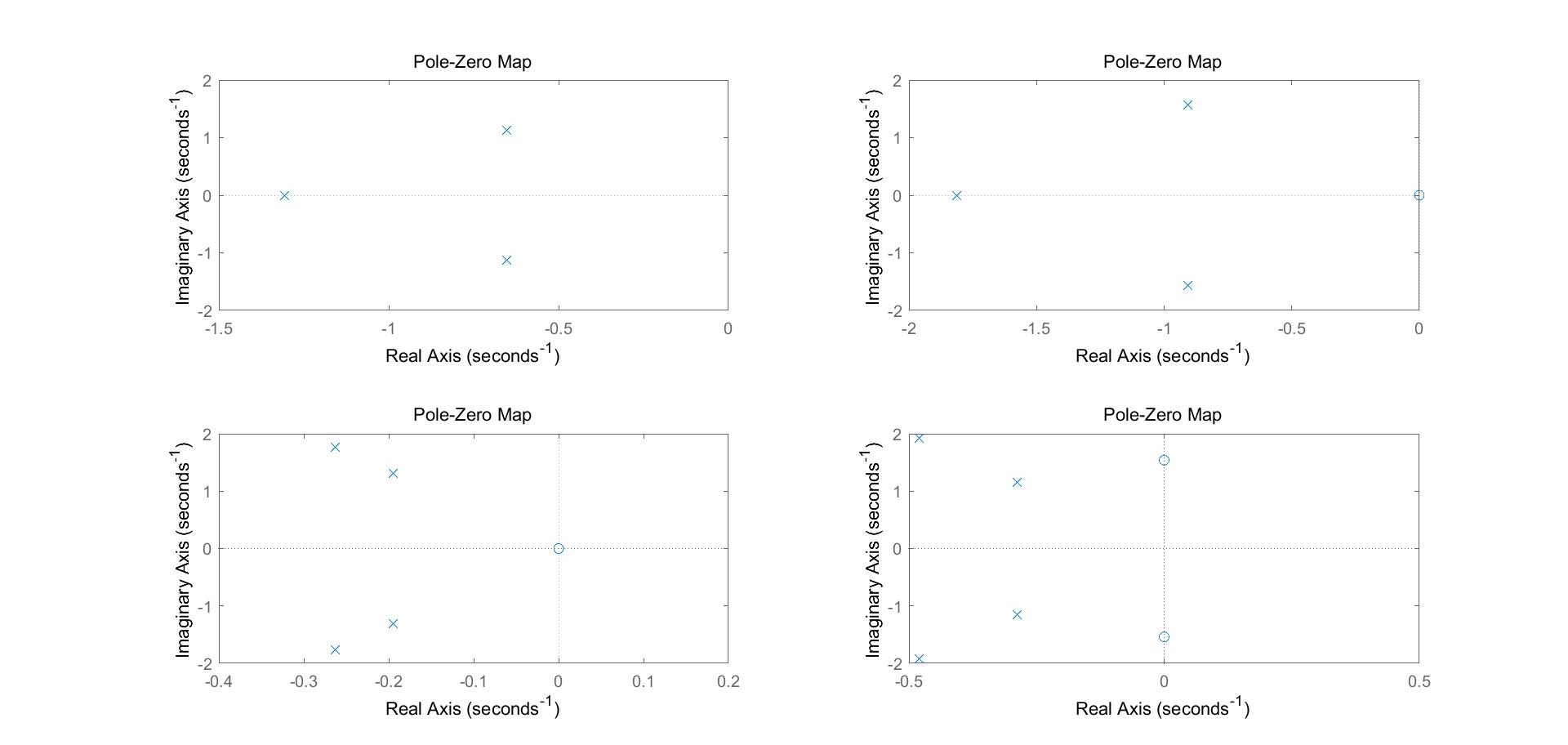（5）定性分析零极点与频率响应$|H(j\omega)|$的关系。
考虑$s=j\omega$：
- 当低通时，$\omega$很小，所以分子不能有$s$项，且必须有常数项，所以低通滤波器没有零点。
- 当高通时，$\omega$很大，所以分母要和分子同阶，故零极点的数目相同才能保证高频时$|H(j\omega)|$接近1。
- 分子分母同阶还有一个有趣的现象是，化简$H(s)$时，会出现常数1，对应在$h(t)$是$\delta(t)$，表明在高频时，$h(t)$的其他分量都与信号卷积为0，只有$\delta(t)$的贡献，所以可以通过。这也是为什么$h(t)$第二、四图中的$t=0$的位置为负的原因，$\delta(t)$画不出来，只能画出其他部分。
- 带阻滤波器具有低通和高通的性质，所以有常数项，也有最高项；而带通滤波器没有低通和高通的性质，故没有常数项和最高项，但有平方项，故在某$\omega$处存在极值，即为通过的频率带。
（6）相位响应$\psi(j\omega)$的分析将在下一个篇幅单独讨论，敬请期待。
2.Digital Filters
a.Low Pass
$$H(z)=\frac {0.2292+0.4584z^{-1}+0.2292z^{-2}}{1-0.2675z^{-1}+0.1843z^{-2}} $$$w_p=0.4\pi ; w_s=0.6\pi;A_p=3dB;A_s=10dB;$
b.High Pass
$$H(z)=\frac {0.2292-0.4584z^{-1}+0.2292z^{-2}}{1+0.2675z^{-1}+0.1843z^{-2}} $$$w_p=0.6\pi ; w_s=0.4\pi;A_p=3dB;A_s=10dB;$
c.Band Pass
$$H(z)=\frac {0.0995-0.1989z^{-2}+0.0995z^{-4}}{1+0.9316z^{-2}+0.3294z^{-4}} $$$w_{p_1}=0.4\pi ;w_{p_2}=0.6\pi ; w_{s_1}=0.3\pi;w_{s_2}=0.7\pi;A_p=3dB;A_s=10dB;$
d.Band Stop
$$H(z)=\frac {0.4733+0.9467z^{-2}+0.4733z^{-4}}{1+0.6469z^{-2}+0.2465z^{-4}} $$$w_{p_1}=0.3\pi ;w_{p_2}=0.7\pi ; w_{s_1}=0.4\pi;w_{s_2}=0.6\pi;A_p=3dB;A_s=10dB;$
Discussion
（1）比较四个数字滤波器的频率响应$|H(j\Omega)|$，$\Omega\subseteq[-2\pi,2\pi]$，横坐标坐标归一化$\pi$。
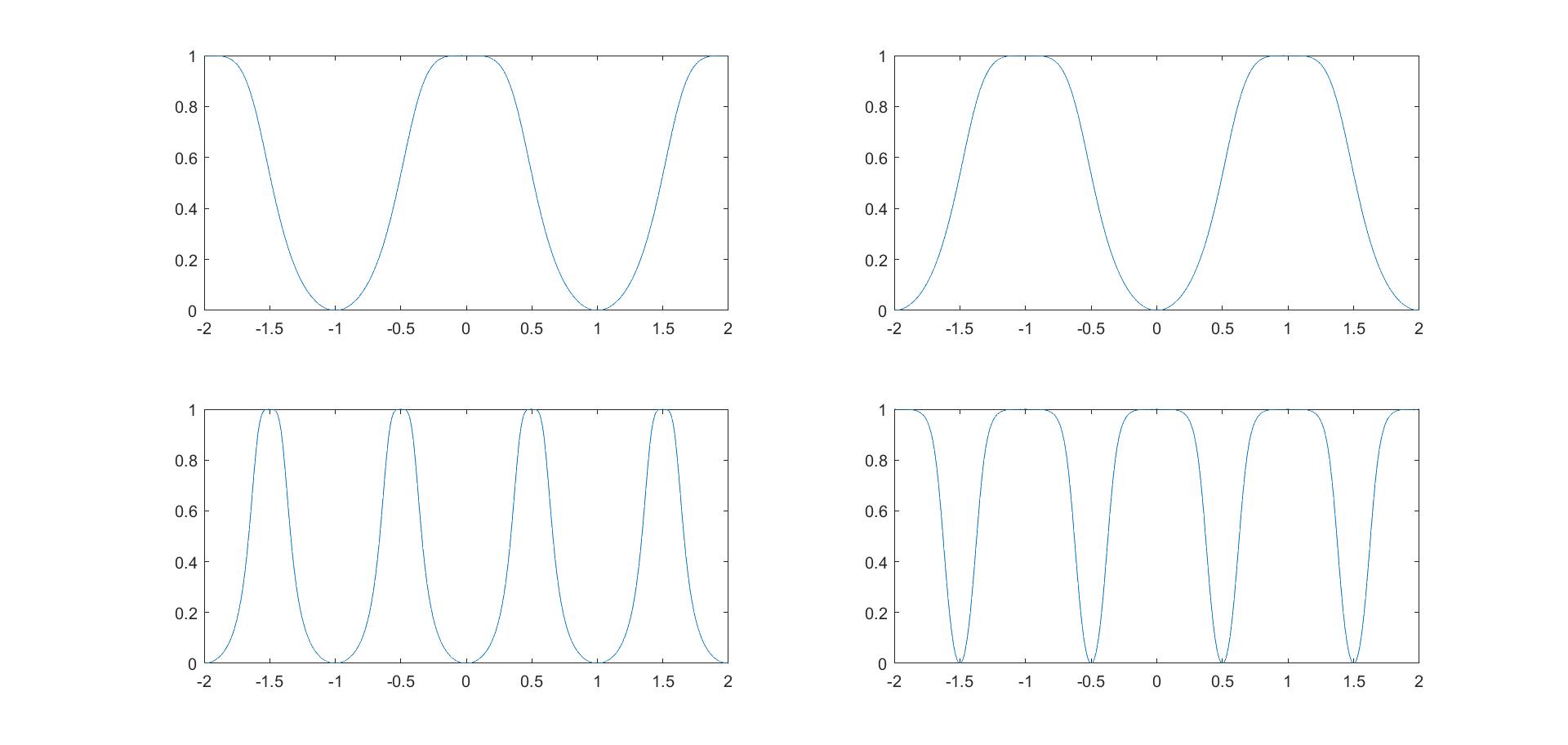（2）比较四个数字滤波器的相位响应$\psi(j\Omega)$
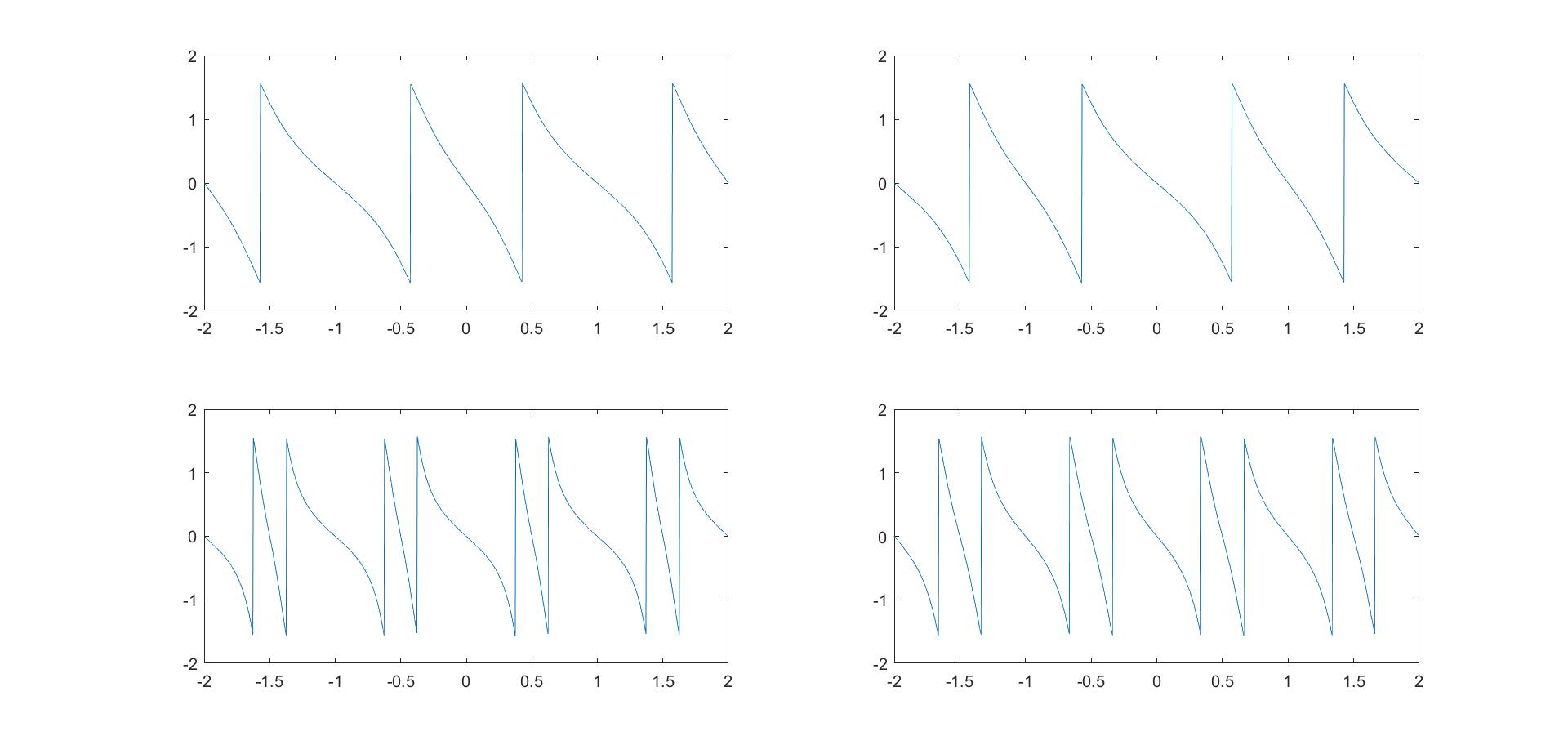
（3）比较四个数字滤波器的单位脉冲响应$h[k]$
（4）比较四个滤波器的零极点分布图
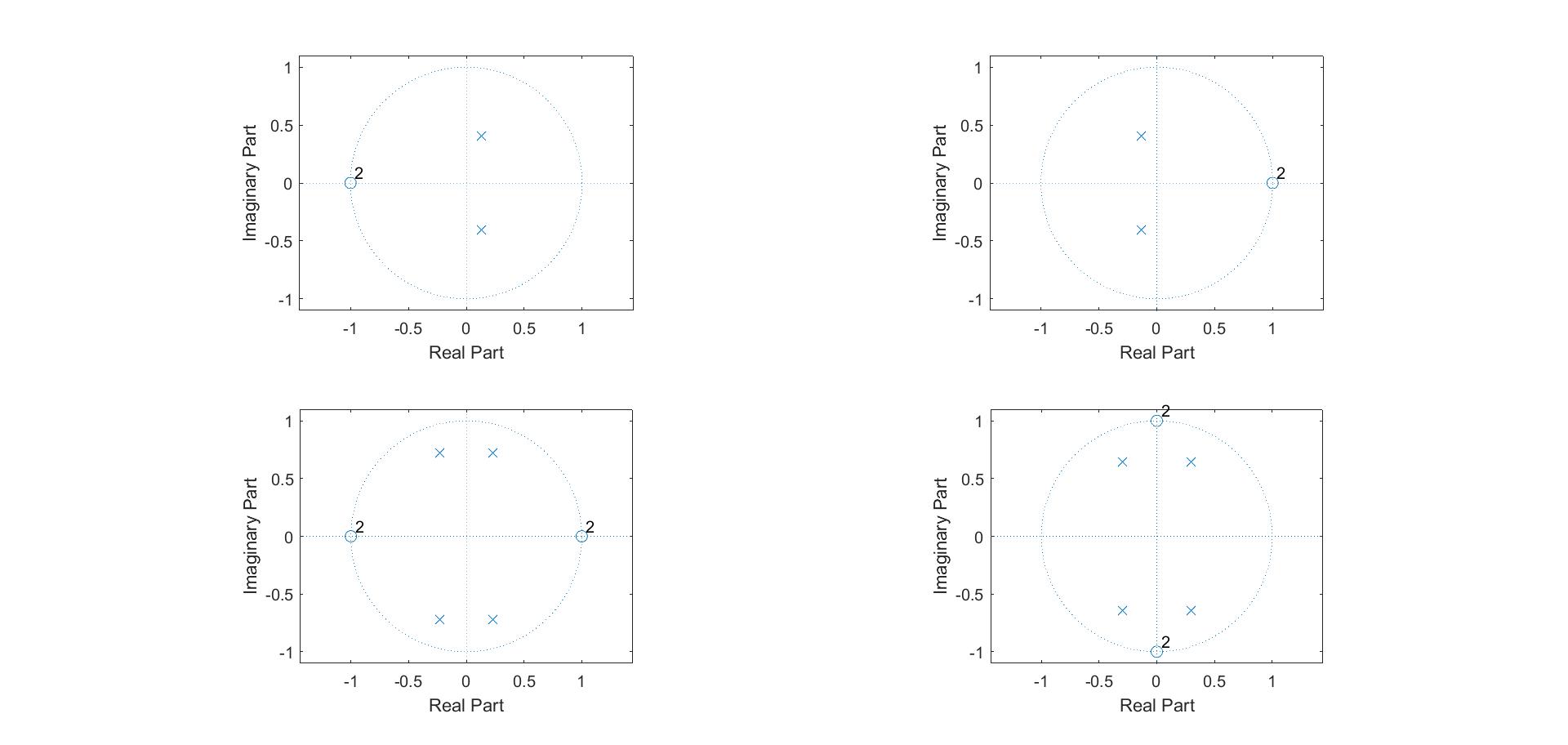（5）定性分析零极点与频率响应$|H(j\Omega)| $的关系。
由零极点可以得到 $$H(j\Omega)=\frac{(z-p_1)(z-p_2)}{(z-z_1)(z-z_2)} $$ 的形式。考虑$z=e^{j\Omega}$，不同的$\Omega$实际对应零极点图中单位圆上的不同位置：
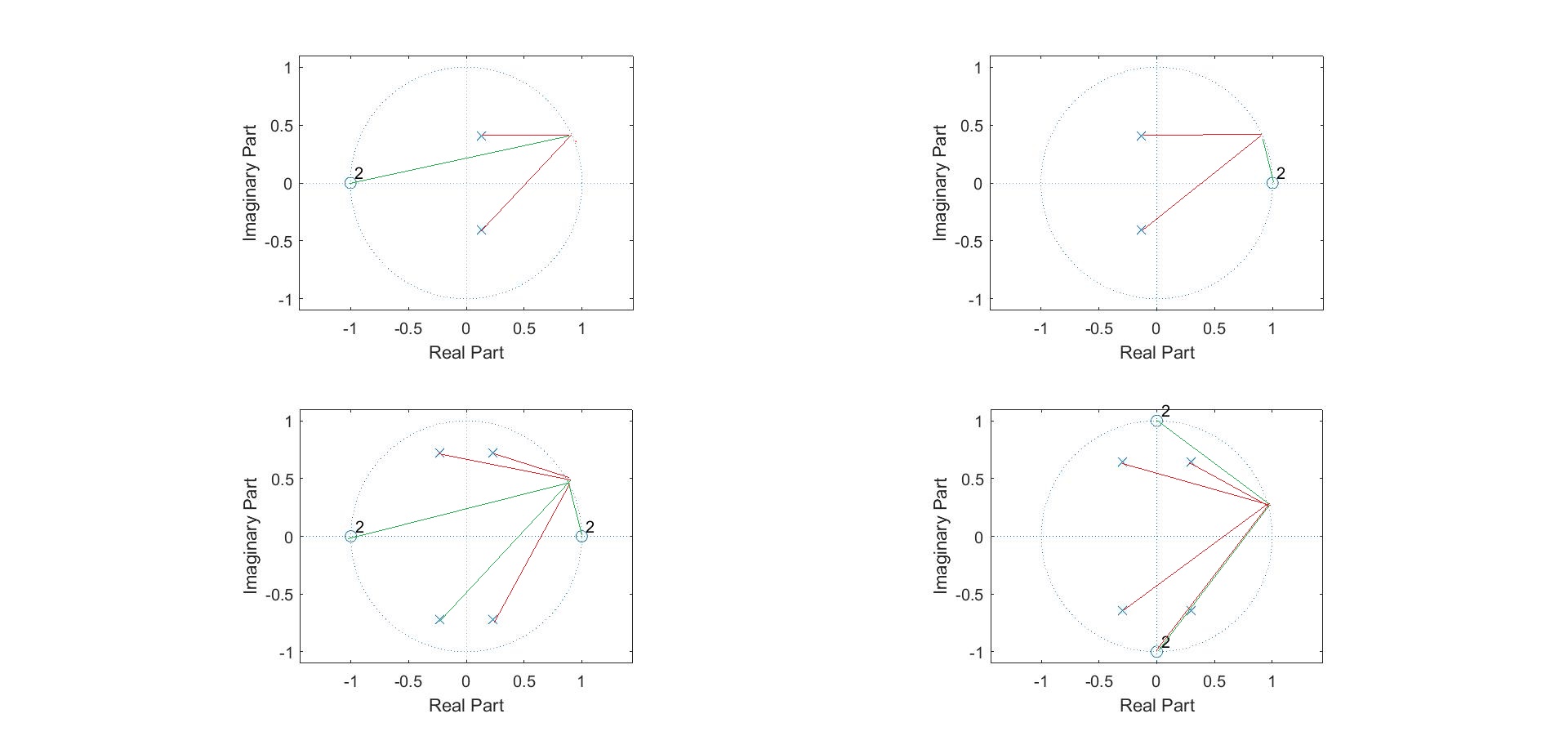
而$|H(j\Omega)|$的大小实际上等价于$$\frac{绿色线段的长度乘积}{红色线段的长度乘积}$$两个零点表示乘两次。因此容易看出：
- $\Omega$为低频0附近，图1图4的结果较大，表示低通和带阻滤波器可以低频通过。而图2图3的结果为零，表示高通和带通滤波器不能低频通过。
- $\Omega$为高频$\pi$附近，图1图3的结果为0，表示低通和带通滤波器不能高频通过。而图2图4的结果较大，表示高通和带阻滤波器可以高频通过。
- 我们可以很容易从零点分布看出哪些频率的波不能通过。极点与x轴的位置会影响$A_p,A_s$的衰减情况。
相位响应$\psi(j\Omega)$的分析将在下一个篇幅单独讨论，敬请期待。感谢中国MOOC学院北京交通大学陈后金老师《数字信号处理》的课程。