Differences between four kinds of IIR filters(B)

摘要：文章重点比较了模拟低通、模拟高通、数字低通、数字高通滤波器的相位响应特性。通过滤波实例直观地看出滤波前后的波形变化，进步一加深相位线性变化对滤波影响的理解。

1. Low Pass Analog Filter

$w_p=0.4\pi ; w_s=0.6\pi;A_p=3dB;A_s=10dB;$

$$ H(s)=\frac {2.232}{s^3+2.614s^2+3.416s+2.232} $$ 

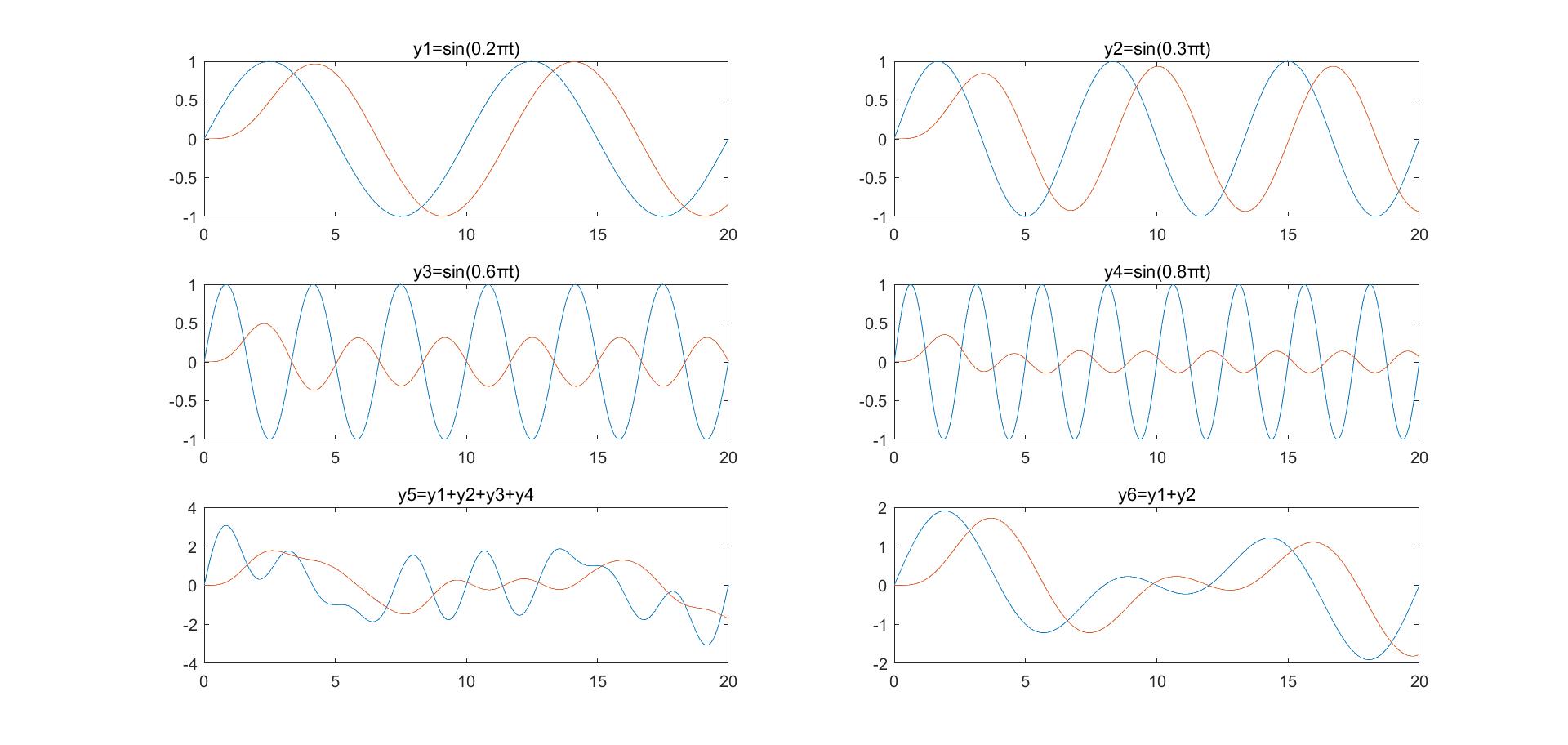
上图分别选取不同频率（$\omega=0.2\pi,0.3\pi,0.6\pi,0.8\pi$）的波通过模拟低通滤波器，图5是所有的组合通过情况，图6是低频的组合通过的情况：

• 随着$\omega$的增大，通过的幅度越来越小；
• 通过的波存在相位延迟，这和相位响应是一致的；
• 图5表示滤波的过程，留下低频成分；
• 图6可以看出低频信号通过滤波器，只有相位移动，原因是$\psi(j\omega)$在$\omega\subseteq[0.2\pi,0.3\pi]$呈现线性变化，故信号不失真。

2. High Pass Analog Filter

$w_p=0.6\pi ; w_s=0.4\pi;A_p=3dB;A_s=10dB;$

$$H(s)=\frac {s^3}{s^3+3.625s^2+6.569s+5.953} $$ 

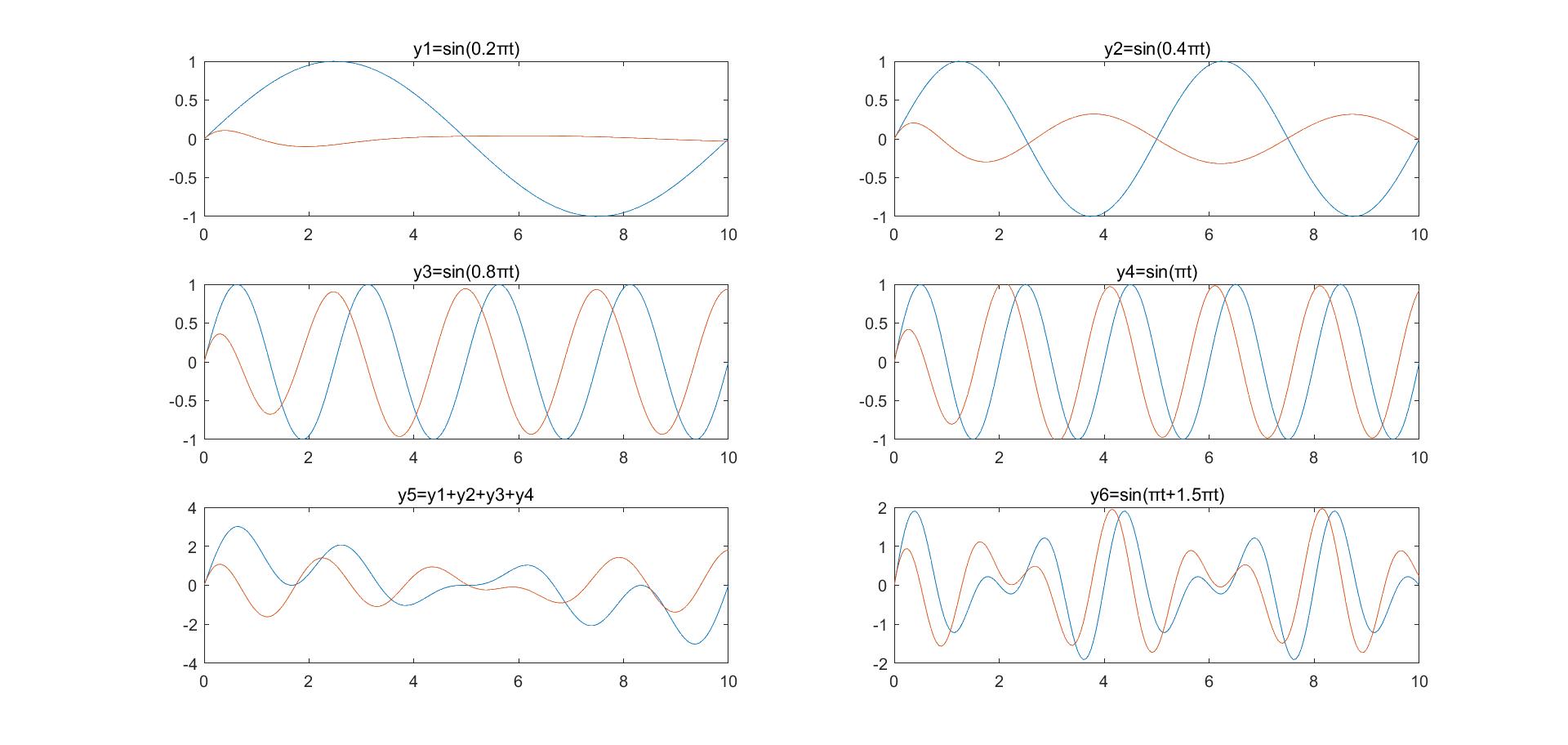
上图分别选取不同频率（$\omega=0.2\pi,0.4\pi,0.8\pi,1.0\pi$）的波通过模拟低通滤波器，图5是所有的组合通过情况，图6是高频的组合通过的情况：

• 随着$\omega$的增大，通过的幅度越来越大，体现高通的特性；
• 通过的波存在相位超前，这和相位响应对应的位置是一致的；
• 图5表示滤波的过程，留下高频频成分；
• 图6可以看出高频信号通过滤波器，形状发生改变，原因是$\psi(j\omega)$在$\omega\subseteq[1.0\pi,1.5\pi]$不呈现线性变化，故信号失真。

3. Low Pass Digital Filter

$w_p=0.4\pi ; w_s=0.6\pi;A_p=3dB;A_s=10dB;$

$$H(z)=\frac {0.2292+0.4584z^{-1}+0.2292z^{-2}}{1-0.2675z^{-1}+0.1843z^{-2}} $$ 

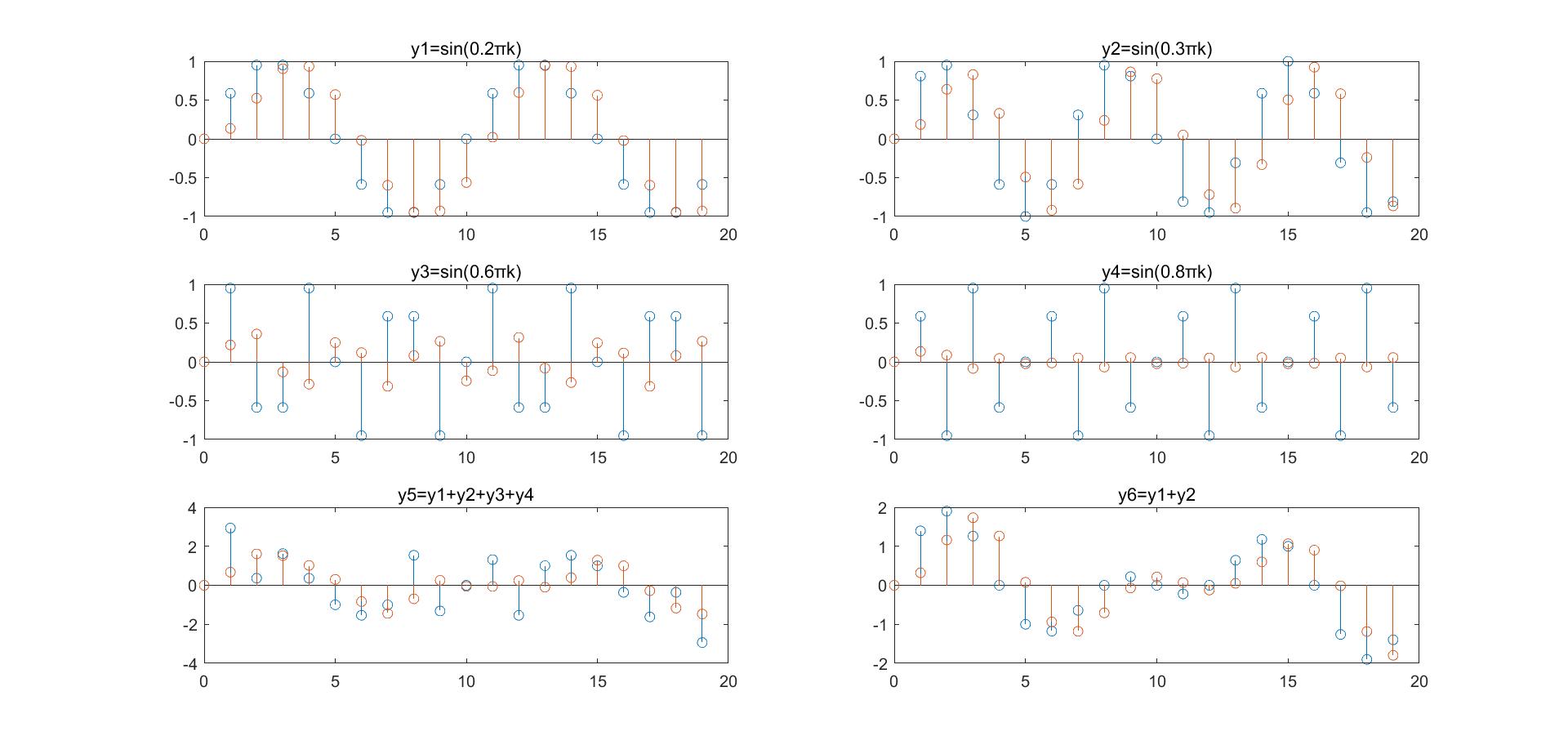
上图分别选取不同频率（$\Omega=0.2\pi,0.3\pi,0.6\pi,0.8\pi$）的波通过数字低通滤波器，图5是所有的组合通过情况，图6是低频的组合通过的情况：

• 随着$\Omega$的增大，通过的幅度越来越小，体现高通的性质；
• 通过的波存在相位延迟，这和相位响应是一致的；
• 图5表示滤波的过程，留下低频成分；
• 图6可以看出低频信号通过滤波器，只有相位移动，原因是$\psi(j\Omega)$在$\Omega\subseteq[0.6\pi,0.8\pi]$呈现线性变化，故信号不失真。

4. Low Pass Digital Filter

$w_p=0.6\pi ; w_s=0.4\pi;A_p=3dB;A_s=10dB;$

$$H(z)=\frac {0.2292-0.4584z^{-1}+0.2292z^{-2}}{1+0.2675z^{-1}+0.1843z^{-2}} $$

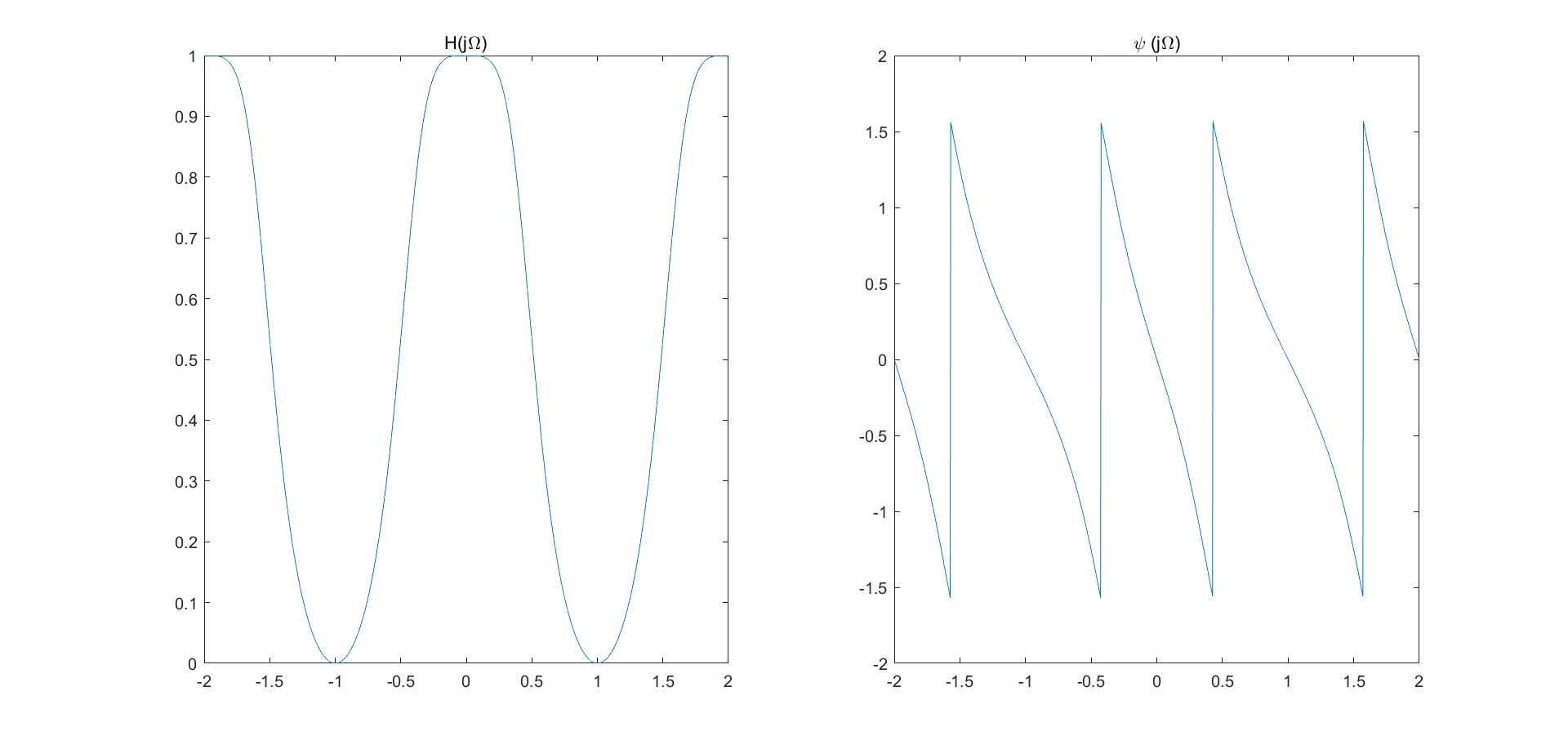
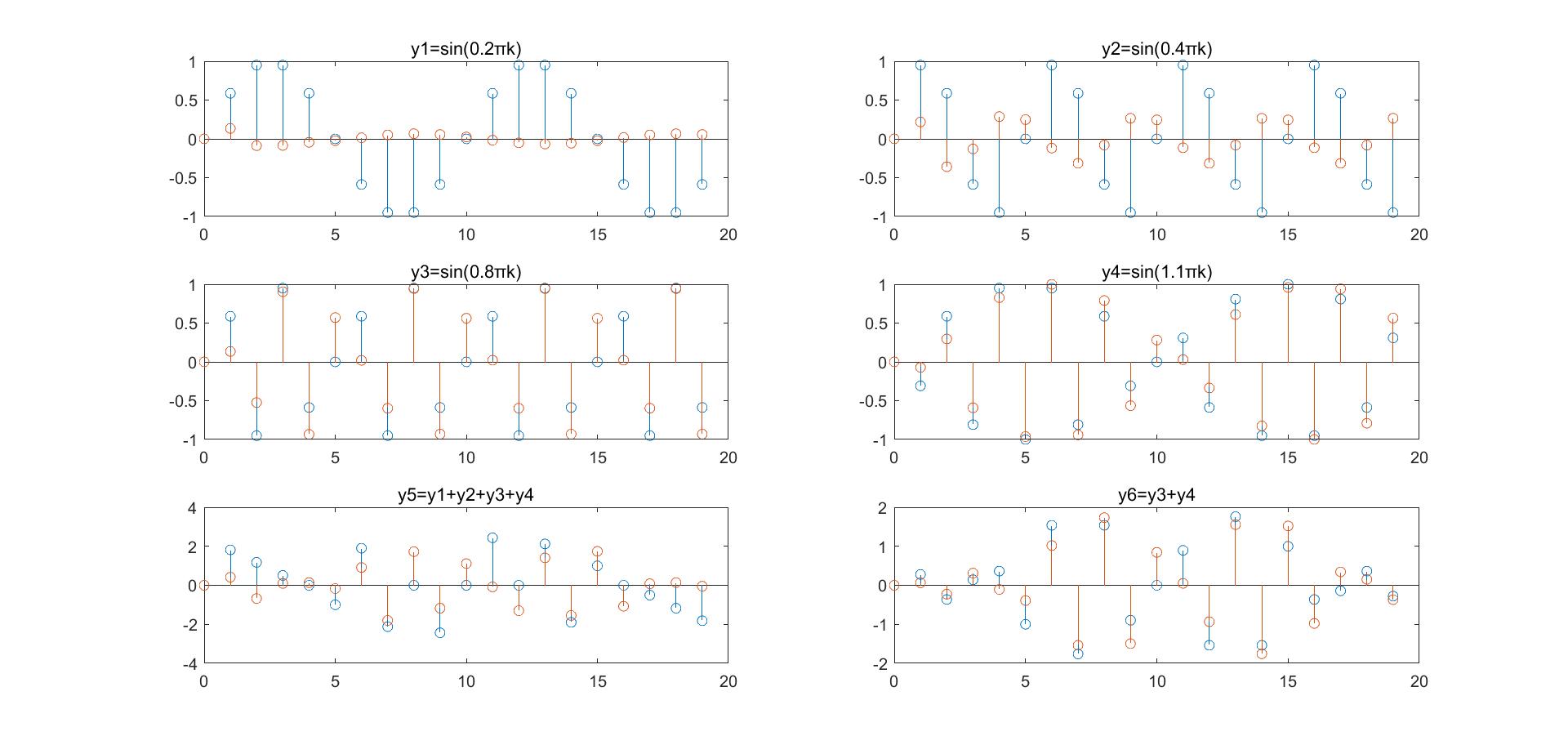
上图分别选取不同频率（$\Omega=0.2\pi,0.4\pi,0.8\pi,1.1\pi$）的波通过数字低通滤波器，图5是所有的组合通过情况，图6是高频的组合通过的情况：

• 随着$\Omega$的增大，通过的幅度越来越大，体现高通的性质；
• 图1~4的波的相位变化不是很明显，理论上是超前的；
• 图5表示滤波的过程，留下高频频成分；
• 图6可以看高频出信号通过滤波器，信号基本上只有相位移动，图形基本不失真，原因是$\psi(j\Omega)$在$\Omega\subseteq[0.8\pi,1.1\pi]$呈现线性变化，故信号不失真。

总结：

1. 滤波器的频率响应$|H(j\omega)|$或$|H(j\Omega)|$决定了哪些频率的波可以通过系统；
2. 滤波器的相位响应$|\psi(j\omega)|$或$|\psi(j\Omega)|$决定了波通过的相位变化，线性变化的相位响应不会改变信号组合的形状。非线性变化的相位响应会改变信号组合的形状，但不会改变单频信号的形状；
3. 在处理如声音这类不容易听出变化的信号，可以采用具有非线性相位变化的滤波器，IIR滤波器能够应付；
4. 在处理如图像这类容易看出变化的信号，宜采用具有线性相位变化的滤波器，因此FIR有限长度滤波器孕育而生。

有关FIR数字滤波器的MATLAB实验敬请期待。感谢中国MOOC学院北京交通大学陈后金老师《数字信号处理》的课程。