摘要：Kronig-Penny模型是能带理论的经典模型，但大多数教科书仅止步于说明能带间隙的产生，而没有返回讨论波函数的定性分布情况。本文第一、二部分罗列了经典的求解过程，第三部分用数值计算的方法，重点讨论了特定能量下的波函数分布，给出直观的呈现，第四部分做定性半定量讨论。
0. Question
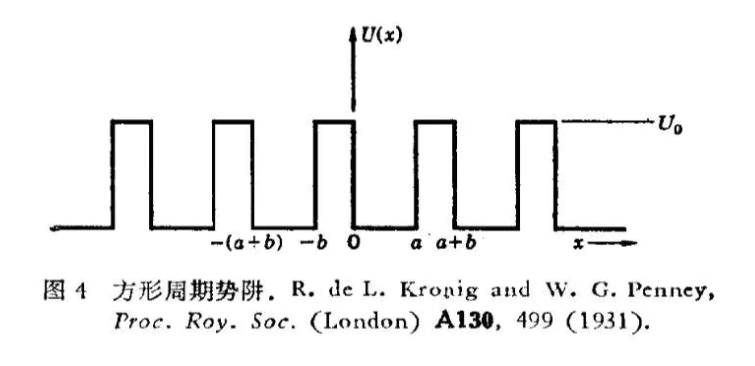存在以上周期势场，求电子波函数分布？最后可以通过$b\to 0,U_0\to \infty,bU_0= 常数$来化简问题。其中的技巧是要用到布洛赫函数的性质：
$$ \psi(x+T)=\psi(x)e^{ikT}$$
用人话表述是：晶体中电子波函数具有调幅的平面波形式。
### 1.Basic Equation
$-b
$0
$$\psi(x)=Ae^{iK x}+Be^{-iK x} ,K^2=\frac{2mE}{\hbar^2}$$
$a
$$\psi(x)=[Ce^{Q (x-a-b)}+De^{-Q (x-a-b)}]e^{ik(a+b)} $$
$x=0$处$\psi(x),\psi(x)'$连续：
$$
A+B=C+D \\
iK(A-B)=Q(C-D)
$$
$x=a$处$\psi(x),\psi(x)'$连续：
$$
Ae^{iK a}+Be^{-iK a}=(Ce^{-Qb}+De^{Q b})e^{ik(a+b)}\\
iK(Ae^{iKa}-Be^{-iKa})=Q(Ce^{-Qb}-De^{Qb})e^{ik(a+b)}
$$
有解条件是系数行列式为0，物理意义是这里的振幅没有归一化，全是成比例的，所以需要可约化。
$$[\frac{(Q^2-K^2)}{2QK}]sinh (Qb)sin(Ka)+cosh(Qb)cos(Ka)=cos(ka+kb)$$
为了简化问题，令$b=0,U_0\to \infty ,Q^2ab/2\equiv P $ ,即为周期性$\delta(x)$势场，也成为狄拉克梳。此时可化为：
$$\frac{P}{Ka}sin(Ka)+cos(Ka)=cos(ka)$$
2.More Details
为了便于数值求解，令$a=1,P=3\pi/2$,系数行列式可化为：
$$\frac{1.5 \pi}{ K}sin(K)+cos(K)=cos(k)$$
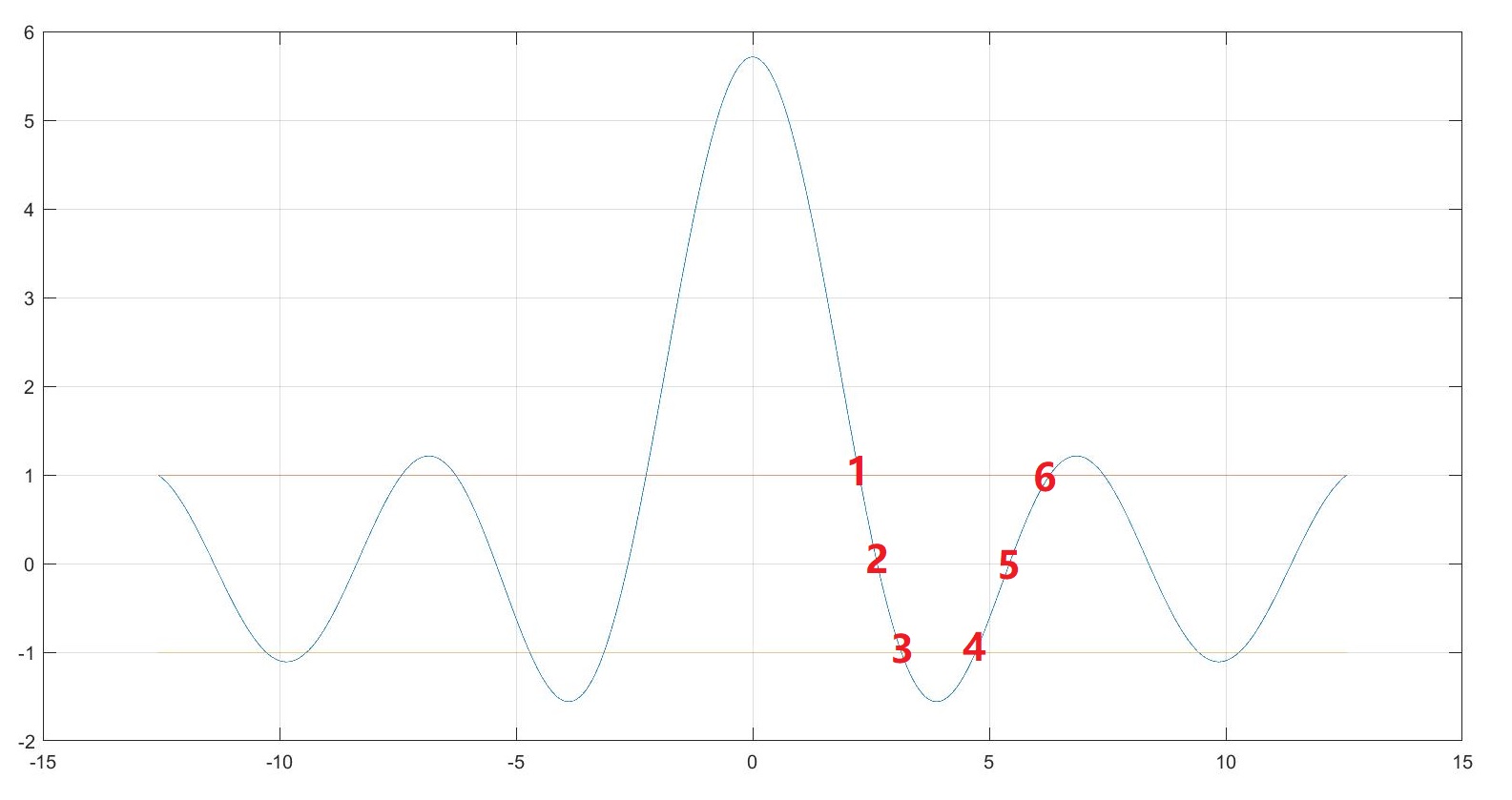
横轴表示$K$(能量)随逐渐变大，但等式右边的值必须介于$[-1,1]$否则得不到波矢量$k$的值，因此$K$的取值是有限制的，这就是解释了为什么会存在禁带。图中我们看到最小的能量在“1”处，对应$K=2.251$，这与自由电子最小能量从零开始是不一样的。“3”和“4”的波矢均为$\pi$，但两者存在能量差，这就是两分立能级间的禁带宽度。能带图如下：
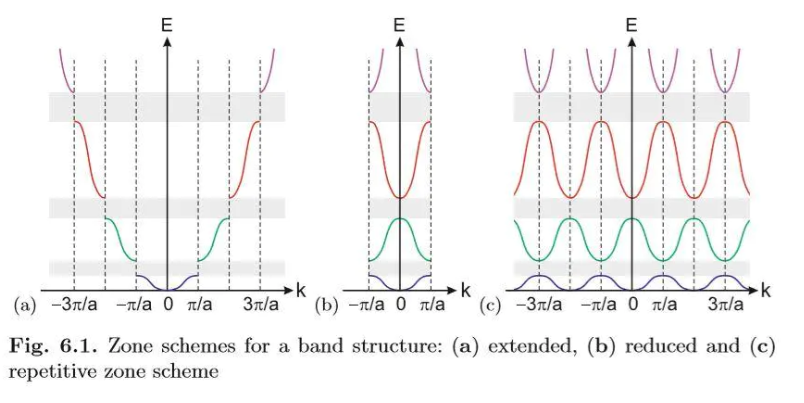
一般我们只看第一布里渊区的能谱图。
3.波函数
为了更直观地表现粒子的运动状态，我们用数值计算“1”-"6"对应一个周期$[0,1]$内的波函数分布$|\psi(x)|^2$。
$$
\begin{array}{c|lcr}
n & \text{K} & \text{cos(k)} & \text{k} \\
\hline
1 & 2.251 & 1 & 0 \\
2 & 2.631 & 0 & \pi/2 \\
3 & 3.141 & -1 & \pi \\
4 & 4.715 & -1& \pi \\
5 & 5.428 & 0 & - \pi/2 \\
6 & 6.280 & 1 & 0\\
\end{array}
$$
$$ \psi(x)=Ae^{iK x}+Be^{-iK x} $$
这里可先令$A=1,b=0.0001$，求得$B$:
$$B=\frac{e^{ik}(ibK-1)+e^{iK}}{e^{ik}(ibK+1)-e^{-iK}}$$
再对$\int_0^1|\psi(x)^2|dx=1$做归一化。
$$\psi(x)=\frac{\psi(x)}{\sqrt E}\\E=1+|B|^2+2sin(K)/K[real(B)*cos(K)+imag(B)*sin(K)]$$
经过简单的数值运算，得到
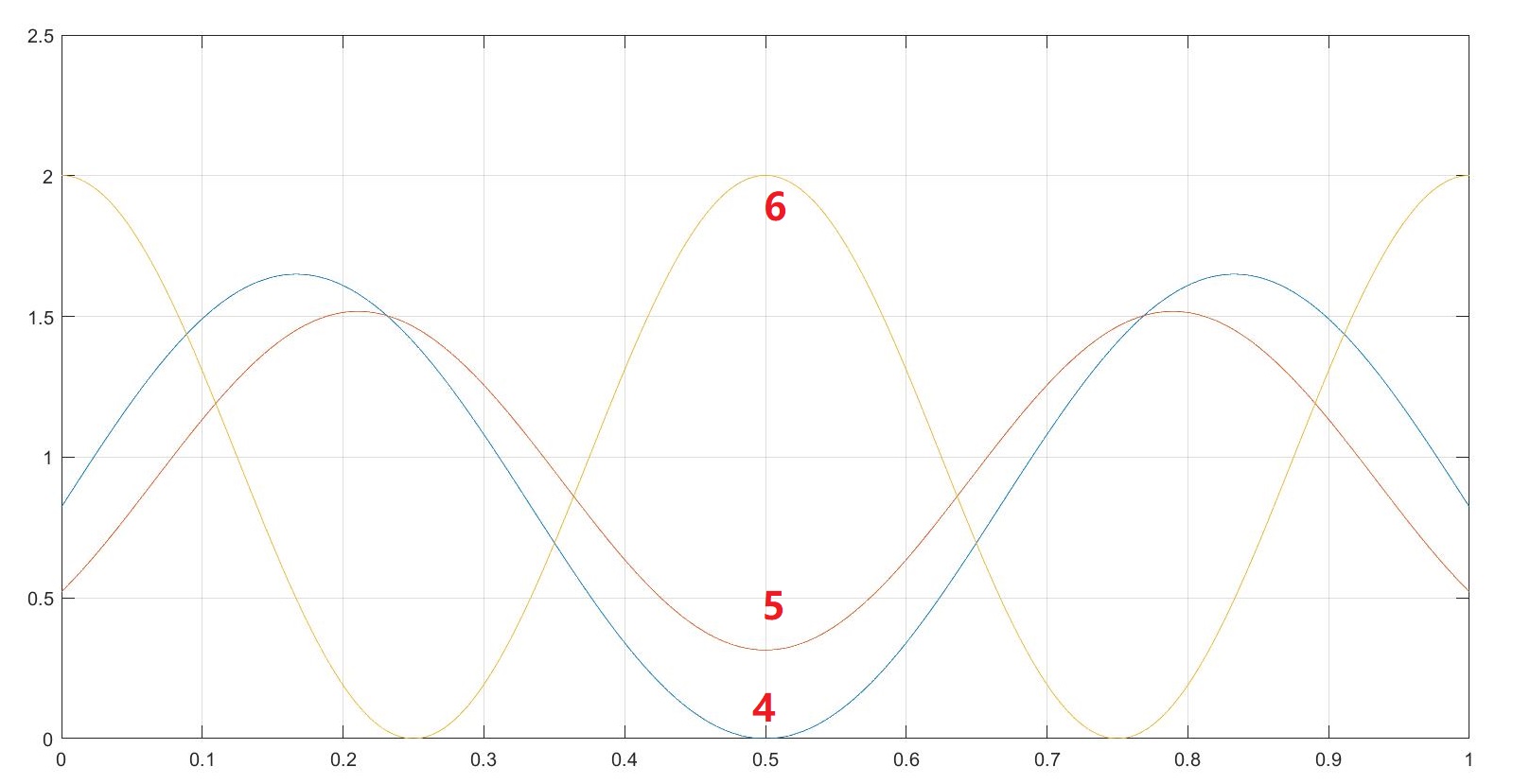
4.Discussion
- 容易看出，第一能带有一个峰，第二能带有两个峰，当能量逐渐增大时，峰越来越往里“挤”；
- 第一能带由低能到高能，$k$由$0\to \pi$。第二能带由低能到高能，$k$由$\pi\to 0$；
- 相同的$k$值可以对应不同能带中对应的能量；
- 最后给个有趣的现象，当第一能带逐渐增大时，在$k=\pi$时有波形的突变，这也是和自由电子很不一样的地方，这也正是狄拉克梳势场的结果：
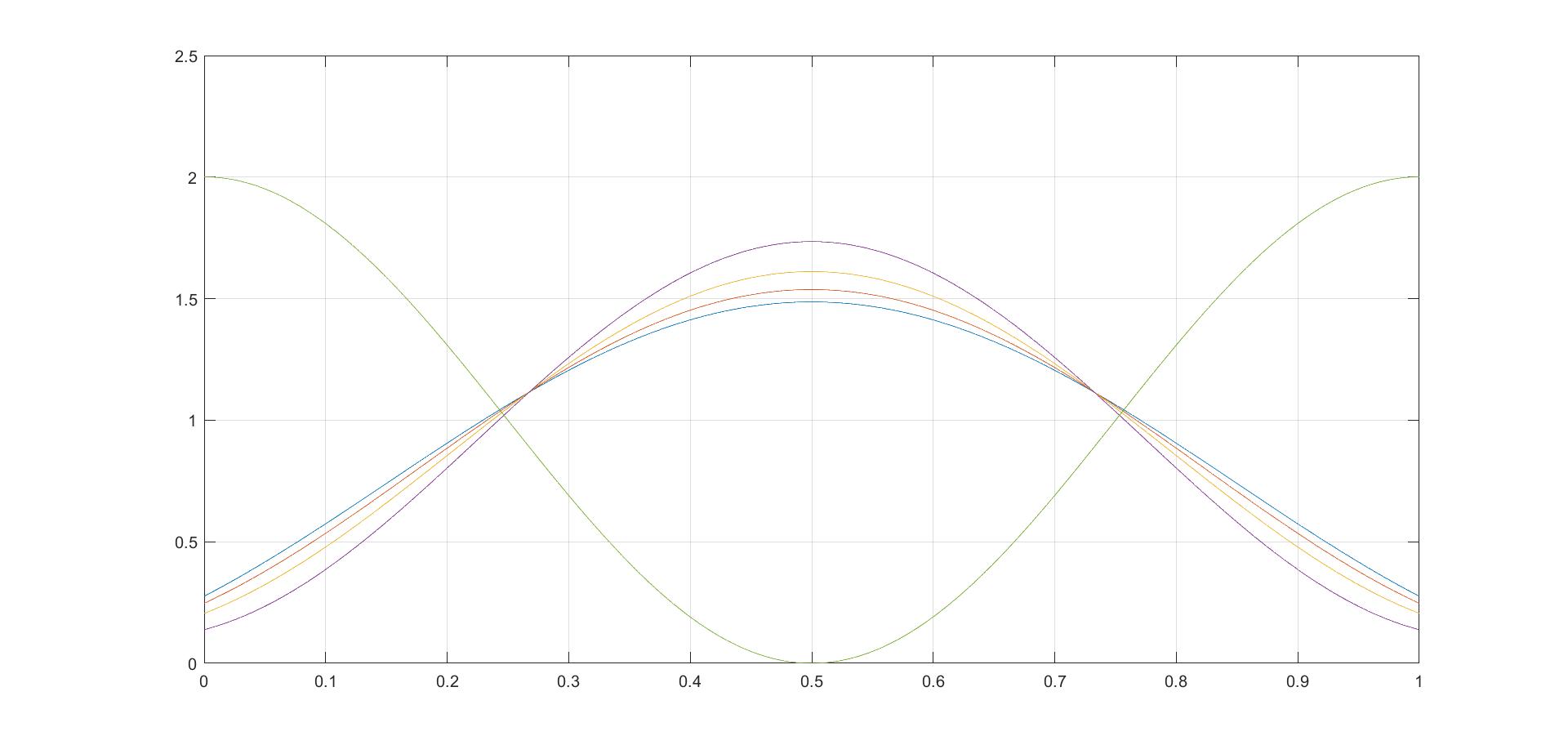结论对其他能带同样适用。
- 另外可以自行体会价带顶和导带底波形的异同点。
存在以上周期势场，求电子波函数分布？最后可以通过$b\to 0,U_0\to \infty,bU_0= 常数$来化简问题。其中的技巧是要用到布洛赫函数的性质：
结论对其他能带同样适用。